
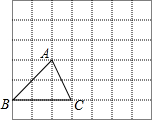
 如图,已知三角形ABC,请根据下列提示作图:
如图,已知三角形ABC,请根据下列提示作图:科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 学生 | 1 | 2 | 3 | 4 | 5 | 6 |
| (1)班的成绩/个 | 77 | 81 | 74 | 84 | 78 | 80 |
| (2)班的成绩/个 | 79 | 77 | 80 | 77 | 79 | 82 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
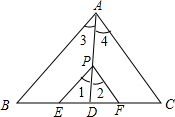 如图所示,已知△ABC中,PE∥AB交BC于E,PF∥AC交BC于F,P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
如图所示,已知△ABC中,PE∥AB交BC于E,PF∥AC交BC于F,P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 国家规定“中小学生每天在校体育活动时间不低于1h”,为此,某市就“每天在校体育活动”时间的问题随机调查了辖区内320名初中学生,根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
国家规定“中小学生每天在校体育活动时间不低于1h”,为此,某市就“每天在校体育活动”时间的问题随机调查了辖区内320名初中学生,根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com