
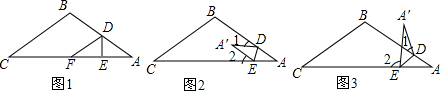
分析 (1)根据折叠的性质得∠DFE=∠A,由已知得∠A=∠C,于是得到∠DFE=∠C,即可得到结论;
(2)先根据四边形的内角和等于360°得出∠A+∠A′=∠1+∠2,再由图形翻折变换的性质即可得出结论;
(3)∠A′ED=∠AED(设为α),∠A′DE=∠ADE(设为β),于是得到∠2+2α=180°,∠1=β-∠BDE=β-(∠A+α),推出∠2-∠1=180°-(α+β)+∠A,根据三角形的内角和得到∠A=180°-(α+β),证得∠2-∠1=2∠A,于是得到结论.
解答 解:(1)根据折叠的性质得:∠DFE=∠A,
∵∠A=∠C,
∴∠DFE=∠C,
∴BC∥DF;
(2)2∠C=∠1+∠2,
理由:∵四边形的内角和等于360°,
∴∠A+∠A′+∠ADA′+∠AEA′=360°.
又∵∠1+∠ADA′+∠2+∠AEA′=360°,
∴∠A+∠A′=∠1+∠2.
又∵∠A=∠A′,
∴2∠A=∠1+∠2,
∵∠A=∠C,
∴2∠C=∠1+∠2;
(3)∠2-∠1=2∠C,
证明如下:由题意得:∠A′ED=∠AED(设为α),∠A′DE=∠ADE(设为β);
∵∠2+2α=180°,∠1=β-∠BDE
=β-(∠A+α),
∴∠2-∠1
=180°-(α+β)+∠A;
∵∠A=180°-(α+β),
∴∠2-∠1=2∠A,
∵∠A=∠C,
∴2∠C=∠2-∠1.
故答案为:2∠C=∠2-∠1.
点评 本题考查了翻折变换的性质,三角形的一个外角等于与它不相邻的两个内角的和,三角形的内角和等于180°,综合题,但难度不大,熟记性质准确识图是解题的关键.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④∠BDC=∠BAC.其中正确的结论有( )
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④∠BDC=∠BAC.其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
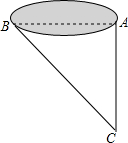 如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.
如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com