练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．小明和小亮同一时刻在阳光下行走，小明身高1.8m，他的影长为2.0m，小亮影长1.8m，则小亮的升高为1.62m．

    分析 设小亮的身高为xm，根据“在同一时刻物高与影长的比相等”得到$\frac{x}{1.8}$=$\frac{1.8}{2.0}$，然后利用比例性质求x即可．

    解答 解：设小亮的身高为xm，
    根据题意得$\frac{x}{1.8}$=$\frac{1.8}{2.0}$，解得x=1.62，
    即小亮的身高为1.62m．
    故答案为1.62m．

    点评 本题考查了相似三角形的应用：通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．如图，一个三角形的纸片ABC，其中∠A=∠C．
    （1）把△ABC纸片按（如图1）所示折叠，使点A落在BC边上的点F处，DE是折痕，说明BC∥DF；
    （2）把△ABC纸片沿DE折叠，当点A落在四边形BCED内时 （如图2），探索∠C与∠1+∠2之间的大小关系，并说明理由；
    （3）当点A落在四边形BCED外时（如图3），∠C与∠1、∠2的关系是2∠C=∠2-∠1．（直接写出结论）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

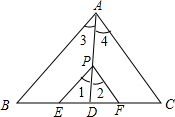    9．如图所示，已知△ABC中，PE∥AB交BC于E，PF∥AC交BC于F，P是AD上一点，且点D到PE的距离与到PF的距离相等，判断AD是否平分∠BAC，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．勾股定理神秘而美妙，它的验证方法多样，其巧妙各有不同，其中“面积法”最为常见，将四个全等的直角三角形如图1摆放时，可以用“面积法”来验证勾股定理；将两个全等的直角三角形按图2摆放时，其中∠DAB=90°，得到梯形DECB，也能验证勾股定理．

    下面是小聪利用图2验证勾股定理的过程，请将其补充完整：
    解：连接DB，由条件可得，四边形DECB是梯形．
    ∴S四边形DECB=$\frac{1}{2}（BC+DE）•EC$=

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

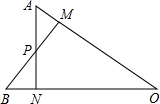    13．如图，AN⊥OB，BM⊥OA，垂足分别是N、M，BM与AN交于点P，若OM=ON，则下列结论不正确的是（　　）
    A．OA=OBB．AM=BN
    C．点P在∠AOB的平分线上D．AM=PM

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．某制药厂两年前生产1吨某种药品的成本是100万元，随着生产技术的进步，现在生产1吨这种药品的成本为81万元，求这种药品的成本平均每年下降的百分率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．函数y=-5x+a+2是关于x的正比例函数，则a=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．国家规定“中小学生每天在校体育活动时间不低于1h”，为此，某市就“每天在校体育活动”时间的问题随机调查了辖区内320名初中学生，根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：
    A组：t＜0.5h；B组：0.5h≤t＜1h；C组：1h≤t＜1.5h；D组：t≥1.5h
    请根据上述信息解答下列问题：
    （1）C组的人数是140；
    （2）本次调查数据的中位数落在C组内；
    （3）若该市辖区内约有32000名初中学生，请你估计其中达国家规定体育活动时间的人约有多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，已知AB∥CD∥EF，AF与BE交于O点，若AF=9，BO=2，OC=1，CE=4，求DF和OD的长．

    查看答案和解析>>

    同步练习册答案