
【题目】已知![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,连接
,连接![]() .
.
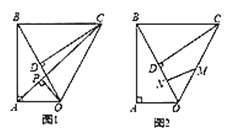
(1)如图,连接![]() ,作
,作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的面积和线段
的面积和线段![]() 的长;
的长;
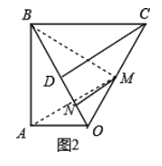
(2)如图,点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的动点(不与点
上的动点(不与点![]() 重合),求
重合),求![]() 周长的最小值.
周长的最小值.
【答案】(1)![]() ,
,![]() ;(2)最小值为
;(2)最小值为![]() .
.
【解析】
(1)利用30°角的性质求出OA,AB,由旋转的性质得到![]() 是等边三角形,根据勾股定理求出AC,再利用面积法可求出
是等边三角形,根据勾股定理求出AC,再利用面积法可求出![]() 面积和OP的值;
面积和OP的值;
(2)如图2,连接BM,AM,根据等边三角形的性质得到BM⊥OC,根据全等三角形的性质得到BM=AB,AO=OM,得到AM被BD垂直平分,即M关于直线BO的对称点为A,连接AC,则C△CMN=AC+MC,于是得到结论.
解:(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
由旋转性质可知:![]() ,
,![]() ,∴
,∴![]() 是等边三角形,
是等边三角形,
∴![]() ;
;
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
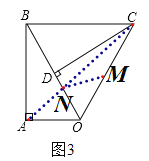
(2)如图2,连接![]() 、
、![]() ,
,
∵![]() 为
为![]() 中点,
中点,![]() 为等边三角形,∴
为等边三角形,∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() 在
在![]() 的中垂线上,
的中垂线上,
∴![]() 被
被![]() 垂直平分,
垂直平分,
即![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,
,
连接![]() ,交
,交![]() 于点
于点![]() ,则此时
,则此时![]() 的周长最小,且
的周长最小,且![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
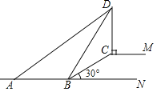
【题目】如图,![]() 是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆
是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆![]() 的顶端
的顶端![]() 处有一探射灯,射出的边缘光线
处有一探射灯,射出的边缘光线![]() 和
和![]() 与水平路面
与水平路面![]() 所成的夹角
所成的夹角![]() 和
和![]() 分别是37°和60°(图中的点
分别是37°和60°(图中的点![]() 均在同一平面内,
均在同一平面内,![]() ).则
).则![]() 的长度约为( )(结果精确到0.1米,)参考数据:(
的长度约为( )(结果精确到0.1米,)参考数据:(![]() =1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. 9.4米B. 10.6米C. 11.4米D. 12.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A城有肥料200吨,B城有肥料300吨.现要把这些肥料全部运往C,D两乡,从A城往C,D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C,D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.设从A城调往C乡肥料x吨.
(1)根据题意,填写下表:
调入地 数量/吨 调出地 | C | D |
A | x | ______ |
B | _____ | ______ |
总计 | 240 | 260 |
(2)给出完成此项调运任务最节省费用的调运方案及所需费用,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y= ![]() 经过圆心H,则反比例函数的解析式为________.
经过圆心H,则反比例函数的解析式为________.
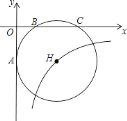
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①,点C是AB中点,CD⊥AB,P是CD上任意一点,由三角形全等的判定方法“SAS”易证△PAC≌△PBC,得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”

(探究)如图②,在平面直角坐标系中,直线y=-![]() x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长
x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长
(应用)如图③
(1)将线段AB绕点A顺时针旋转90°得到线段AB′,请在图③网格中画出线段AB;
(2)若存在一点P,使得PA=PB′,且∠APB′≠90°,当点P的横、纵坐标均为整数时,则AP长度的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,点D是![]() 的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
(1)求证:AF⊥EF.
(2)直接回答:
①已知AB=2,当BE为何值时,AC=CF?
②连接BD、CD、OC,当∠E等于多少度时,四边形OBDC是菱形?
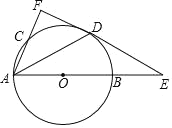
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+5与x轴交于A,点B,与y轴交于点C,过点C作CD⊥y轴交抛物线于点D,过点B作BE⊥x轴,交DC延长线于点E,连接BD,交y轴于点F,直线BD的解析式为y=﹣x+2.
(1)写出点E的坐标;抛物线的解析式.
(2)如图2,点P在线段EB上从点E向点B以1个单位长度/秒的速度运动,同时,点Q在线段BD上从点B向点D以![]() 个单位长度/秒的速度运动,当一个点到达终点时,另一个点随之停止运动,当t为何值时,△PQB为直角三角形?
个单位长度/秒的速度运动,当一个点到达终点时,另一个点随之停止运动,当t为何值时,△PQB为直角三角形?
(3)如图3,过点B的直线BG交抛物线于点G,且tan∠ABG=![]() ,点M为直线BG上方抛物线上一点,过点M作MH⊥BG,垂足为H,若HF=MF,请直接写出满足条件的点M的坐标.
,点M为直线BG上方抛物线上一点,过点M作MH⊥BG,垂足为H,若HF=MF,请直接写出满足条件的点M的坐标.
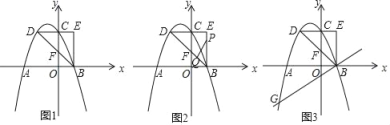
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com