
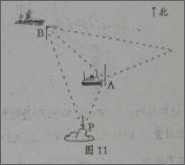
 如图,P处是一个小岛,从P处发现北偏东25°方向、距离为15
如图,P处是一个小岛,从P处发现北偏东25°方向、距离为15| 2 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
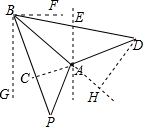 作DH⊥AB于点H.在直角△ADH中,∠DAH=180°-120°=60°,设AD=60t,则BD=60
作DH⊥AB于点H.在直角△ADH中,∠DAH=180°-120°=60°,设AD=60t,则BD=60| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| DH |
| BD |
30
| ||
60
|
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
| A、顶点坐标是(2,0) |
| B、顶点坐标是(0,2) |
| C、顶点坐标是(-2,0) |
| D、顶点坐标是(0,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 我国2014年的外汇储备接近了4万亿美元,将这个数据用科学记数法可记作( )
我国2014年的外汇储备接近了4万亿美元,将这个数据用科学记数法可记作( )| A、0.4×1013 |
| B、4×1012 |
| C、4×1013 |
| D、40000×108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com