
分析 (1)由题意知,抛物线与x轴的两交点坐标为(1,0)、(3,0),用交点式求解析式即可;
(2)先求出A、B两点坐标,然后用待定系数法求直线解析式;
(3)①根据题意列不等式组,求解集即可;
②首先表示出E,F,G,H各点的坐标,进而根据平行四边形的性质求出t的值即可.
解答 解:(1)∵抛物线y=-x2+bx+c,当1<x<3时,y值为正,当x<1或x>3时,y值为负.
∴抛物线与x轴的两交点坐标为(1,0)、(3,0),
∴y=-(x-1)(x-3)=-x2+4x-3;
(2)∵直线y=kx+b(k≠0)与抛物线交于点A($\frac{1}{2}$,m)和B(4,n),
∴m=-($\frac{1}{2}$)2+4×$\frac{1}{2}$-3=-$\frac{5}{4}$,n=-42+4×4-3=-3,
∴A($\frac{1}{2}$,-$\frac{5}{4}$)B(4,-3),
把A、B两点坐标代入直线y=kx+b(k≠0)得:$\left\{\begin{array}{l}{\frac{1}{2}k+b=-\frac{5}{4}}\\{4k+b=-3}\end{array}\right.$,
解得:k=-$\frac{1}{2}$,b=-1,
∴y=-$\frac{1}{2}$x-1;
(3)①∵平行于y轴的直线x=t和x=t+2分别交线段AB于E、F,交抛物线于H、G,
∴$\left\{\begin{array}{l}{t≥\frac{1}{2}}\\{t+2≤4}\end{array}\right.$,
解得:$\frac{1}{2}$≤t≤2;
②存在;
∵HE∥FG,
∴当HE=FG时,四边形EFGH是平行四边形,
∵HE=-t2+4t-3+$\frac{1}{2}$t+1=-t2+$\frac{9}{2}$t-2,FG=-(t+2)2+4(t+2)-3+$\frac{1}{2}$(t+2)+1=-t2+$\frac{1}{2}$t+3;
∴-t2+$\frac{9}{2}$t-2=-t2+$\frac{1}{2}$t+3;
解得:t=$\frac{5}{4}$,
∵t=$\frac{5}{4}$在$\frac{1}{2}$≤t≤2的解集内,
∴当t=$\frac{5}{4}$时,四边形EFGH是平行四边形.
点评 此题主要考查了二次函数的综合应用以及待定系数法求一次函数和二次函数解析式以及平行四边形的性质,根据点的坐标性质得出E,F,G,H点的坐标,进而利用平行四边形对边相等得出是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷(解析版) 题型:解答题
先阅读下面的内容,
例题:若 ,求:
,求: 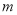 和
和 的值.
的值.
∵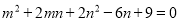
∴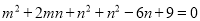
∴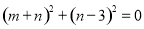
∴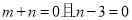
∴
根据你的观察,探究下面问题
(1)若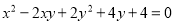 ,求
,求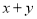 的值.
的值.
(2)试说明不论 取什么数,多项式
取什么数,多项式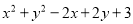 的值总是正数
的值总是正数
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
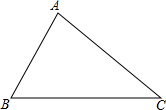 如图,A、B、C三点表示三个村庄,线段AB、BC、AC表示村村通公路,为解决村民手机信号问题,移动通信公司计划新建一座基站和一间物资储备室.要求基站到这三个村庄的距离相等,物资储备室到这三条村村通公路的距离相等,请你在图中用尺规作图的方式确定基站和物资储备室的位置(分别用点P和Q表示,作图不写作法,但要保留作图痕迹).
如图,A、B、C三点表示三个村庄,线段AB、BC、AC表示村村通公路,为解决村民手机信号问题,移动通信公司计划新建一座基站和一间物资储备室.要求基站到这三个村庄的距离相等,物资储备室到这三条村村通公路的距离相等,请你在图中用尺规作图的方式确定基站和物资储备室的位置(分别用点P和Q表示,作图不写作法,但要保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com