
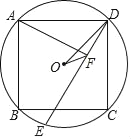
【题目】如图,⊙O为正方形ABCD的外接圆,E为弧BC上一点,AF⊥DE于F,连OF、OD.
(1)求证:AF=EF;
(2)若![]() ,求sin∠DOF的值.
,求sin∠DOF的值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)如图,过B作BG⊥AF于G,连接BE、OB,只要证明四边形BGEF是矩形,△ABG≌△DAF即可解决问题;
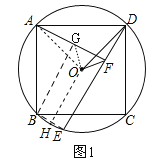
(2)作OH⊥BE于H,连接AO,GO.首先证明OH垂直平分线段FG,再证明∠DOF=∠DAF,△FOG是等腰直角三角形即可解决问题;
试题解析:证明:(1)如图,过B作BG⊥AF于G,连接BE、OB.∵AF⊥DE,∴∠AGB=∠AFD=90°,∴∠BAF+∠ABG=90°.∵四边形ABCD是正方形,∴BD为⊙O的直径,AD=AB,∠BAD=90°,∴∠DAF+∠BAF=90°,∠BED=90°,∴∠ABG=∠DAF,∴△ABG≌△DAF,∴BG=AF.∵∠BED=∠BGF=∠AFE=90°,∴四边形GBEF是矩形,∴EF=BG,∴AF=EF;
(2)作OH⊥BE于H,连接AO,GO.
∵OH⊥BE,∴BH=HE,∴OH垂直平分线段BE.∵四边形GBEF是矩形,∴BE=GF,BE∥GF,∴OH垂直平分线段FG,∴OG=OF.∵∠AOD=∠AFD=90°,∴A、D、F、O四点共圆,∴∠DOF=∠DAF,∠OFG=∠ADO=45°,∴△FOG是等腰直角三角形,∴FG=![]() OF.∵EF=BG=AF=2
OF.∵EF=BG=AF=2![]() OF,∴AF=2FG,AG=FG=DF,设DF=a,则AF=2a,AD=
OF,∴AF=2FG,AG=FG=DF,设DF=a,则AF=2a,AD=![]() a,∴sin∠DOF=sin∠DAF=
a,∴sin∠DOF=sin∠DAF=![]() =
=![]() .
.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
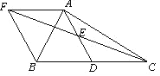
【题目】如图,在![]() 中,D是BC的中点,E是AD的中点,过点A作
中,D是BC的中点,E是AD的中点,过点A作![]() ,AF与CE的延长线相交于点F,连接BF.
,AF与CE的延长线相交于点F,连接BF.
(1)求证:四边形AFBD是平行四边形;
(2)①若四边形AFBD是矩形,则![]() 必须满足条件_________;
必须满足条件_________;
②若四边形AFBD是菱形,则![]() 必须满足条件_________.
必须满足条件_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
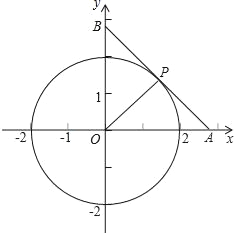
【题目】如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画圆,P是⊙O上一动点且在第一象限内,过点P作⊙O的切线,与x、y轴分别交于点A、B.
(1)求证:△OBP与△OPA相似;
(2)当点P为AB中点时,求出P点坐标;
(3)在⊙O上是否存在一点Q,使得以Q,O,A、P为顶点的四边形是平行四边形.若存在,试求出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
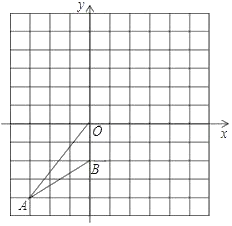
【题目】如图,已知,在平面直角坐标系中,A(﹣3,﹣4),B(0,﹣2).
(1)△OAB绕O点旋转180°得到△OA1B1,请画出△OA1B1,并写出A1,B1的坐标.
(2)判断以A,B,A1,B1为顶点的四边形的形状,请直接在答卷上填写答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
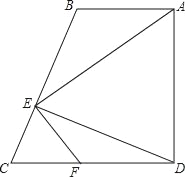
【题目】如图,在四边形ABCD中,AB∥CD,∠ADC=90°,DE⊥BC于E,连AE,FE⊥AE交CD于点F.
(1)求证:△AED∽△FEC;
(2)若AB=2![]() ,求DF的值;
,求DF的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
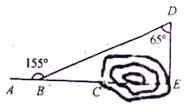
【题目】为了打通抚松到万良的最近公路,在一座小山的底部打通隧道.甲、乙两施工队按如图所示进行施工,甲施工队沿AC方向开山修路,乙施工队在这座小山的另一边E处沿射线CA方向同时施工.从AC上的一点B,取∠ABD=155°,经测得BD=1200m,∠D=65°,求开挖点E与点B之间的距离(结果精确到1m).
【参考数据:![]() ,
, ![]() ,
, ![]() .】
.】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小华两名射箭运动员在赛前的某次测试中射箭10次,成绩及各统计图如下图、表所示:
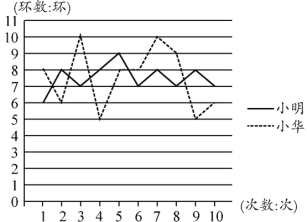
若让你选择其中一名参加比赛则你选择的运动员是:__________,理由是:_________________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com