
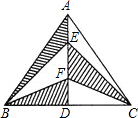
 如图,在△ABC中,AB=AC,点D是BC中点,若BC=5,AD=4,则图中阴影部分的面积为5.
如图,在△ABC中,AB=AC,点D是BC中点,若BC=5,AD=4,则图中阴影部分的面积为5. 分析 根据等腰三角形的性质可知本图是轴对称图形,对称轴是AD所在的直线.所以阴影部分的面积为全面积的一半,由轴对称图形的性质知,BD=$\frac{1}{2}$BC=2.5,AD是三角形的高,AD=4,S△ABC=10,从而得到阴影部分的面积为5.
解答 解:∵AB=AC,
∴△ABC是等腰三角形,
∵点D是BC中点,
∴AD⊥BC,
∴△ABD、△ACD关于AD对称,△BEF与△CEF关于AD对称,
∴S△DFB=S△DFC,S△EBF=S△ECF,S△BE=S△ACE,
∴S阴=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$BC×AD=$\frac{1}{2}$×$\frac{1}{2}$×5×4=5.
故答案为5.
点评 本题考查了等腰三角形的性质,通过观察看出三角形BEF与三角形CEF关于AD对称,面积相等是解决本题的关键.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为MN(点M、N分别在边AC、BC上),给出以下判断:
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为MN(点M、N分别在边AC、BC上),给出以下判断:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠BAC=90°,BC=5cm,AC=3cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中阴影部分)的面积为2πcm2.
如图,在△ABC中,∠BAC=90°,BC=5cm,AC=3cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中阴影部分)的面积为2πcm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com