
分析 (1)先算除法和乘法,再算减法;
(2)利用乘法分配律简算;
(3)先算乘方,和括号里面的运算,再算乘除,最后算减法.
解答 解:(1)原式=$-4×\frac{3}{2}-\frac{3}{5}×30$
=-6-18
=-24;
(2)原式=$(\;\frac{3}{4}-\frac{5}{6}+\frac{4}{9}\;)×(-36)$
=-27+30-16
=-13;
(3)原式=$-1-(-\frac{1}{2})×\frac{1}{3}×(2-16)$
=$-1-\frac{7}{3}$
=$-\frac{10}{3}$.
点评 此题考查有理数的混合运算,掌握运算顺序,正确判定运算符号计算即可.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:解答题
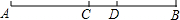 如图,点C是线段AB的中点.
如图,点C是线段AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
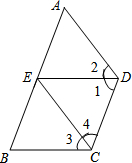 如图,AB∥DC,∠1=∠B,∠2=∠3.
如图,AB∥DC,∠1=∠B,∠2=∠3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+x-1=0 | B. | x2+1=0 | C. | x2-x+2=0 | D. | $\frac{x}{x-1}=\frac{1}{x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
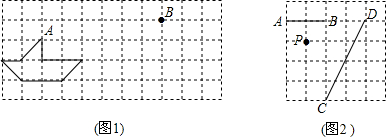
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com