
 如图,四边形ABCD中,AC、BD为对角线,△ABC为等边三角形,∠ADC=30°,AD=2,BD=3,则CD的长为
如图,四边形ABCD中,AC、BD为对角线,△ABC为等边三角形,∠ADC=30°,AD=2,BD=3,则CD的长为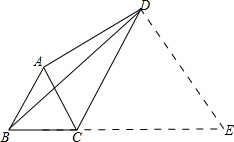
|
| 5 |
| 5 |
| 5 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
| 8 |
| 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
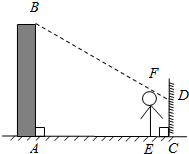 李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.
李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.查看答案和解析>>
科目:初中数学 来源: 题型:
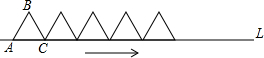 一个边长是1厘米的等边△ABC,将它沿直线L作顺时针方向的翻动,到达图示中最右边三角形的位置,试在A、B、C三个顶点中选一个点,求该点所经过的路程是多少厘米?(精确到0.01厘米)
一个边长是1厘米的等边△ABC,将它沿直线L作顺时针方向的翻动,到达图示中最右边三角形的位置,试在A、B、C三个顶点中选一个点,求该点所经过的路程是多少厘米?(精确到0.01厘米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com