
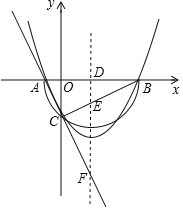
【题目】已知二次函数y=x2+bx+c+1的图象与x轴交于点A(x1,0)、B(x2,0),且x1<x2,与y轴的负半轴交于点C.
(1)当b=1时,求c的取值范围;
(2)如果以AB为直径的半圆恰好过点C,求c的值;
(3)在(2)的条件下,如果二次函数的对称轴l与x轴、直线BC、直线AC的延长线分别交于点D、E、F,且满足DE=2EF,求二次函数的表达式.
【答案】(1)c<﹣1;(2)c的值为﹣2;(3)y=![]() .
.
【解析】
(1)有两个交点则△=0,从而可解;
(2)直径所对的圆周角为直角,再利用斜边中线等于斜边一半可解;
(3)由平行得相似,从而列比例式可解.
(1)已知二次函数y=x2+bx+c+1的图象与x轴交于点A(x1,0)、B(x2,0),当b=1时,
令x2+bx+c+1=0,则△=b2﹣4(c+1)=1﹣4c﹣4>0
∴![]() ,
,
考虑点C在负半轴,则c+1<0,
∴c<﹣1.
当b=1时,求c的取值范围是c<﹣1.
(2)∵C(0,c+1),
令x2+bx+c+1=0,解得点A(![]() ,0),点B(
,0),点B(![]() ,0),
,0),
如果以AB为直径的半圆恰好过点C,则由直径所对的圆周角为直角,得∠ACB=90°,二次函数的对称轴l与x轴交于点D,则D(![]() ,0),
,0),
∴CD=![]() ,即
,即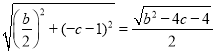 ,化简得c2+3c+2=0,
,化简得c2+3c+2=0,
∴c=﹣2或c=﹣1(舍).
答:c的值为﹣2.
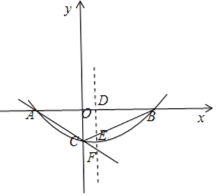
(3)设EF=k,DE=2K,
∵DE∥OC,
∴△DEB~△OCB,
∴![]() ,
,
∴![]() ,
,
∵OC∥DF,
∴△AOC~△ADF
∴![]() ,
,
∴![]() ,
,
∵AD=BD,
∴![]()
又∵x1x2=﹣1,
∴![]() ,
,
∴
∴二次函数的表达式为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).

请解答下列问题:
(1)请补全条形统计图和扇形统计图;
(2)在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?
(3)若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爸爸想送小明一个书包和一辆自行车作为新年礼物,在甲、乙两商场都发现同款的自行车单价相同,书包单价也相同,自行车和书包单价之和为452元,且自行车的单价比书包的单价4倍少8元.
(1)求自行车和书包单价各为多少元;
(2)新年来临赶上商家促销,乙商场所有商品打八五折(即8.5折)销售,甲全场购物毎满100元返购物券30元(即不足100元不返券,满100元送30元购物券,满200元送60元购物券),并可当场用于购物,购物券全场通用.但爸爸只带了400元钱,如果他只在同一家商场购买看中的两样物品,在哪一家买更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某高科技公司生产一种矩形新型材料板,其长宽之比为 3∶2,每张材料板的成本 c与它的面积成正比例。每张材料板的销售价格 y与其宽 x 之间满足我们学习过的某种函数关系(即一次函数、反比例函数和二次函数关系中的一种),下表记录了该工厂生产、销售该材料板一些数据:
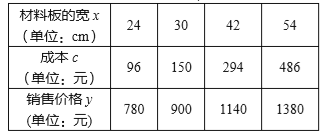
(1)求一张材料板的销售格 y 其宽 x 之间的函数关系式 (不必写出自变的取值范围)
(2)若一张材料板的利润 w 为销售价格 y与成本 c 的差
①请直接写出一张材料板的利润 w 其宽 x 之间的函数关系 (不必写出自变的取值范围)
②当材料板的宽为多少时,一张材料板的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
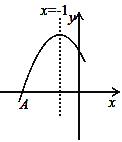
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论:①abc<0 ②b2﹣4ac>0 ③4b+c<0 ④若B(﹣![]() ,y1)、C(﹣
,y1)、C(﹣![]() ,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
其中正确的结论是(填写代表正确结论的序号)__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月22日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
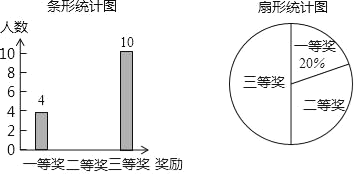
(1)求本次竞赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)如果该校八年级有800人,请你估计获奖的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
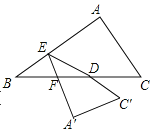
【题目】如图,在Rt△ABC中,AC=3,AB=4,D为斜边BC的中点,E为AB上一个动点,将△ABC沿直线DE折叠,A,C的对应点分别为![]() ,
,![]() ,
,![]() 交BC于点F,若△BEF为直角三角形,则BE的长度为______.
交BC于点F,若△BEF为直角三角形,则BE的长度为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com