
| A. | 4 | B. | 2 | C. | 5 | D. | 2或4 |
分析 分两种情况:①点D在BC边上,如图1,由AD是△ABC边BC上的高,得到∠ADB=90°,根据sin∠BAD=$\frac{BD}{AB}$=$\frac{3}{5}$,求得BD=3,于是得到结论;②点D在直线BC上,如图2,同理得到结论.
解答  解:①点D在BC边上,如图1,∵AD是△ABC边BC上的高,
解:①点D在BC边上,如图1,∵AD是△ABC边BC上的高,
∴∠ADB=90°,
∵sin∠BAD=$\frac{BD}{AB}$=$\frac{3}{5}$,
∵AB=5,
∴BD=3,
∴BC=BD+CD=4,;
②点D在直线BC上,如图2,
∵AD是△ABC边BC上的高,
∴∠ADB=90°,
∵sin∠BAD=$\frac{BD}{AB}$=$\frac{3}{5}$,
∵AB=5,
∴BD=3,
∴BC=BD-CD=2.
故选D.
点评 本题考查了解直角三角形的知识,勾股定理,注意熟练掌握锐角三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:解答题
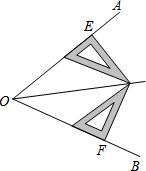 用两只完全相同的三角尺在∠AOB的内部如图摆放,两只三角尺较短的直角边必须分别与∠AOB的两边重合,且含30°角的顶点恰好也重合于点C.则射线OC即为∠AOB的角平分线.试利用所学知识说明射线OC平分∠AOB的理由.
用两只完全相同的三角尺在∠AOB的内部如图摆放,两只三角尺较短的直角边必须分别与∠AOB的两边重合,且含30°角的顶点恰好也重合于点C.则射线OC即为∠AOB的角平分线.试利用所学知识说明射线OC平分∠AOB的理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13(1-x)2=20 | B. | 20(1-x)2=13 | C. | 20(1+x)2=13 | D. | 13(1+x)2=20 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
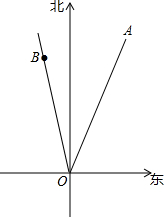 2014年第10号台风“麦德姆”,是2014年度对我国破坏性最大的一次台风,“麦德姆”台风从福建登陆后一路北上,在青岛荣成再次登陆.如图所示,某时,台风“麦德姆”的中心在点O沿北偏东20°的方向以30km/h的速度移动,在点O北偏西10°的方向距离O点360km处有一个小岛B.如果台风中心的最大风力为14级,每远离台风中心20千米风力减弱一级,小岛A的风力达到四级或四级以上,则称其受台风影响.
2014年第10号台风“麦德姆”,是2014年度对我国破坏性最大的一次台风,“麦德姆”台风从福建登陆后一路北上,在青岛荣成再次登陆.如图所示,某时,台风“麦德姆”的中心在点O沿北偏东20°的方向以30km/h的速度移动,在点O北偏西10°的方向距离O点360km处有一个小岛B.如果台风中心的最大风力为14级,每远离台风中心20千米风力减弱一级,小岛A的风力达到四级或四级以上,则称其受台风影响.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com