
【题目】(1)、菱形![]() 的边长1,面积为
的边长1,面积为![]() ,则
,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
(2)、如图,ABCD是正方形,E是CF上一点,若DBEF是菱形,则∠EBC=

【答案】(1)B;(2)15°.
【解析】
试题分析:(1)在菱形ABCD中,设AO=x,BO=y,根据菱形的性质得出: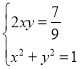 求出x、y的值即可求出AC+BD的值.
求出x、y的值即可求出AC+BD的值.
(2)过D作DG垂直于CF,垂足为G,由正方形的性质可得出正方形的四条边相等,且四个角为直角,三角形BCD为等腰直角三角形,可得出∠BDC与∠DBC都为45°,设正方形的边长为1,根据勾股定理求出BD的长为![]() ,即菱形的四条边为
,即菱形的四条边为![]() ,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为
,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为![]() ,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC∠DBE求出度数即可.
,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC∠DBE求出度数即可.
(1)在菱形ABCD中,设AO=x,BO=y,
根据菱形的性质得出: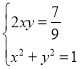 解得
解得![]()
∴AC+BD=2(x+y)=2×![]() =
=![]() .
.
故选B.
(2)过D作DG⊥CF,垂足为G,如图所示:
∵四边形ABCD为正方形,
∴∠CBD=∠CDB=45°,∠BCD=90°,
设正方形ABCD的边长为1,即AB=BC=CD=AD=1,
∴根据勾股定理得:BD=![]() ,
,
∵四边形BEFD为菱形,
∴BE=EF=DF=BD=![]() ,
,
又BD∥EF,DG⊥FC,
∴BD⊥DG,即∠BDG=90°,
∴∠CDG=∠BDG∠BDC=90°45°=45°,又∠DGC=90°,
∴△DCG为等腰直角三角形,又DC=1,
∴DG=DCsin45°=![]() ,
,
又DF=![]() ,
,
在Rt△DFG中,由DG=![]() DF,
DF,
∴∠F=30°,
∴∠DBE=30°,
则∠EBC=∠DBC∠DBE=45°30°=15°.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】关于x、y的多项式(m﹣2)![]() +(n+3)xy2+3xy﹣5.
+(n+3)xy2+3xy﹣5.
(1)若原多项式是五次多项式,求m、n的值;
(2)若原多项式是五次四项式,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
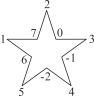
【题目】如图,将-2,-1,0,1,2,3,4,5,6,7这10个数分别填写在五角星中每两条线的交点处(每个交点处只填写一个数),将每一条线上的4个数相加,共得5个数,设为a1,a2,a3,a4,a5.
(1)求![]() (a1+a2+a3+a4+a5)的值;
(a1+a2+a3+a4+a5)的值;
(2)交换其中任何两位数的位置后,![]() (a1+a2+a3+a4+a5)的值是否改变?并说明理由.
(a1+a2+a3+a4+a5)的值是否改变?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区某中学体育组因高中教学需要本学期购进篮球和排球共80个,共花费5800元,已知篮球的单价是80元/个,排球的单价是50元/个.
(1)篮球和排球各购进了多少个(列方程组解答)?
(2)因该中学秋季开学准备为初中也购买篮球和排球,教学资源实现共享,体育组提出还需购进同样的篮球和排球共40个,但学校要求花费不能超过2810元,那么篮球最多能购进多少个(列不等式解答)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是直线m上两个定点,C是直线n上一个动点,且m∥n.以下说法:
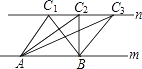
①△ABC的周长不变;
②△ABC的面积不变;
③△ABC中,AB边上的中线长不变.
④∠C的度数不变;
⑤点C到直线m的距离不变.
其中正确的有________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
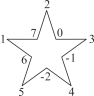
【题目】如图,将-2,-1,0,1,2,3,4,5,6,7这10个数分别填写在五角星中每两条线的交点处(每个交点处只填写一个数),将每一条线上的4个数相加,共得5个数,设为a1,a2,a3,a4,a5.
(1)求![]() (a1+a2+a3+a4+a5)的值;
(a1+a2+a3+a4+a5)的值;
(2)交换其中任何两位数的位置后,![]() (a1+a2+a3+a4+a5)的值是否改变?并说明理由.
(a1+a2+a3+a4+a5)的值是否改变?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+3与x轴交于A,B两点,点A在点B的左侧.
(1)求A,B两点的坐标和此抛物线的对称轴;
(2)设此抛物线的顶点为C,点D与点C关于x轴对称,求四边形ACBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com