Question

12．一座拱型桥，桥下的水面宽度AB是20米，拱高CD是4米，若水面上升至EF=10米，则水面上升了多少？

（1）若把它看作抛物线的一部分，在坐标系中（如图①），可设抛物线的表达式为y=ax²+c．请你填空：
a=-$\frac{1}{25}$，c=4，CG=3米．
（2）若把它看作圆的一部分，可构造图形（如图②）请你计算水面上升高度CG．

Answer 1

分析 （1）设抛物线的解析式为y=ax²+c（a≠0），再根据垂径定理求出A，D的坐标，代入抛物线的解析式求出a、c的值，再把x=5代入即可得出y的值，进而得出CG的长；
（2）设圆的半径是r米，在Rt△OCB中，易知r²=（r-4）²+10²，求出r的值，在Rt△OGF中根据勾股定理求出OG的长，进而可得出CG的长．

解答 解：（1）设抛物线的解析式为y=ax²+c（a≠0），
∵AB是20米，
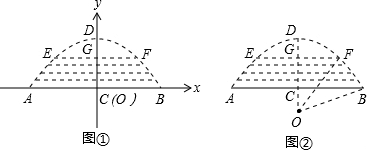
∴AC=10米，拱高CD是4米，
∴A，D的坐标分别是（-10，0），（0，4）
把这两点的坐标代入解析式得，
$\left\{\begin{array}{l}100a+c=0\\ c=4\end{array}\right.$，解得a=-$\frac{1}{25}$，c=4，
则解析式是y=-$\frac{1}{25}$x²+4．
把x=5代入解析式解得y=3，
∴CG=3米．
故答案为：-$\frac{1}{25}$，4，3；

（2）设圆的半径是r米，在Rt△OCB中，
∵OB²=BC²+OC²，即r²=（r-4）²+10²，解得r=14.5，
∴OF=14.5，GF=5，OC=14.5-4=10.5，
∴OG²=OF²-GF²，即OG²=14.5²-5²=185.25，
∴CG=OG-OC=$\sqrt{185.25}$-10.5=（$\frac{\sqrt{741}}{2}$-10.5）米．．

点评 本题考查的是垂径定理的应用及二次函数的应用，熟知垂径定理及用待定系数法求二次函数的解析式是解答此题的关键．