
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点.
两点.
(1)求线段AB的长度;
(2)若点![]() 在第二象限,且△
在第二象限,且△![]() 为等腰直角三角形,求点
为等腰直角三角形,求点![]() 的坐标;
的坐标;

【答案】(1)5(2)(-3,7)(-7,4)(-![]() ,
,![]() )
)
【解析】
(1)先求出A,B的坐标,根据勾股定理,得到AB的长;
(2)分三种情况分别进行讨论.
解:(1)当x=0,得y=3,
当y=0,x=-4,
∴A(-4,0),B(0,3),即OA=4,OB=3,
∴根据勾股定理AB=5;
(2)①过点A作C1A⊥AB,截取AC1=AB,此时△AC1B是等腰直角三角形,

过C1作C1D1⊥x轴于D1,此时Rt△C1D1A≌Rt△AOB,
∴C1D1=OA=4,AD1=OB=3,OD1=7,
∴C1(-7,4);
②过点B作C2B⊥AB,截取BC2=AB,此时△AC2B是等腰直角三角形,

过C2作C2D2⊥y轴于D2,此时Rt△C2D2B≌Rt△BOA,
∴C2D2=OB=3,BD2=OA=4,OD2=7,
∴C2(-3,7);
③以AB为腰,作等腰直角△AC3B,
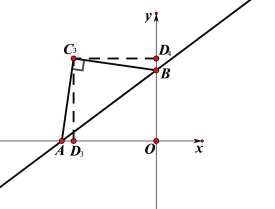
过C3作C3D3⊥OA,作C3D4⊥OB,此时Rt△C3D3A≌Rt△C3D4B,四边形C3D3OD4是正方形,
∴AD3=BD4,
∴OA-AD3=OB+BD4,即4-AD3=3+BD4,
∴AD3=BD4=![]() ,
,
∴OD3=4-![]() ,OD4=3+
,OD4=3+![]() =
=![]() ,
,
∴C3(-![]() ,
,![]() ).
).
故答案为:(1)5;(2)(-3,7)(-7,4)(-![]() ,
,![]() )
)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )
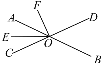
A. 95° B. 65°
C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,每个小正方形边长都是1.

(1)按要求作图: △ABC关于![]() 轴对称的图形△
轴对称的图形△![]() ;
;
(2)将点![]() 先向上平移
先向上平移![]() 个单位,再向右平移
个单位,再向右平移![]() 个单位得到点
个单位得到点![]() 的坐标为 ;
的坐标为 ;
(3)△![]() 的面积为 ;
的面积为 ;
(4)若![]() 为
为![]() 轴上一点,连接
轴上一点,连接![]()
![]() ,则△
,则△![]() 周长的最小值为 .
周长的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车行驶时的耗油量为![]() 升/千米,如图是油箱剩余油量
升/千米,如图是油箱剩余油量![]() (升)关于加满油后行驶的路程
(升)关于加满油后行驶的路程![]() (千米)的函数图象.
(千米)的函数图象.
(1)根据图象,直接写出汽车行驶![]() 千米时,油箱内的剩余油量为 升,加满油时油箱的油量为 升;
千米时,油箱内的剩余油量为 升,加满油时油箱的油量为 升;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)计算该汽车在剩余油量![]() 升时,已行驶的路程.
升时,已行驶的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴被折成![]() ,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2009将与圆周上的数字_________重合。
,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2009将与圆周上的数字_________重合。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数图象的对称轴为直线x=2,顶点为点C,直线y=x+m与该二次函数的图象交于点A,B两点,其中点A的坐标为(5,8),点B在y轴上.
(1)求m的值和该二次函数的表达式.P为线段AB上一个动点(点P不与A,B两点重合),过点P作x轴的垂线,与这个二次函数的图象交于点E.
①设线段PE的长为h,求h与x之间的函数关系式,并写出自变量x的取值范围.
②若直线AB与这个二次函数图象的对称轴的交点为D,求当四边形DCEP是平行四边形时点P的坐标.
(2)若点P(x,y)为直线AB上的一个动点,试探究:以PB为直径的圆能否与坐标轴相切?如果能请求出点P的坐标,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣ ![]() x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N. 
(1)用b的代数式表示顶点M的坐标;
(2)当tan∠MAN=2时,求此二次函数的解析式及∠ACB的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com