
【题目】如图,已知二次函数图象的对称轴为直线x=2,顶点为点C,直线y=x+m与该二次函数的图象交于点A,B两点,其中点A的坐标为(5,8),点B在y轴上.
(1)求m的值和该二次函数的表达式.P为线段AB上一个动点(点P不与A,B两点重合),过点P作x轴的垂线,与这个二次函数的图象交于点E.
①设线段PE的长为h,求h与x之间的函数关系式,并写出自变量x的取值范围.
②若直线AB与这个二次函数图象的对称轴的交点为D,求当四边形DCEP是平行四边形时点P的坐标.
(2)若点P(x,y)为直线AB上的一个动点,试探究:以PB为直径的圆能否与坐标轴相切?如果能请求出点P的坐标,如果不能,请说明理由.
【答案】
(1)解: A的坐标为(5,8)在直线y=x+m上,
∴8=5+m,
∴m=3,
∴直线AB解析式为y=x+3,
∴B(0,3),
设抛物线解析式为y=a(x﹣2)2+k,
∵点A,B在抛物线上,
∴ ![]() ,
,
∴ ![]() ,
,
∴抛物线解析式为y=(x﹣2)2﹣1=x2﹣4x+3,顶点C(2,﹣1)
①∵点P在线段AB上,
∴P(x,x+3)(0≤x≤5),
∵PE⊥x轴,交抛物线与E,P(x,x+3),
∴E(x,x2﹣4x+3),
∴h=PE=x+3﹣(x2﹣4x+3)=﹣x2+5x,(0≤x≤5)
②∵直线AB与这个二次函数图象的对称轴的交点为D,
∴D(2,5),
∴DC=6,
∵四边形DCEP是平行四边形,
∴PE=DC=6,
∵PE=|﹣x2+5x|,
Ⅰ、当0≤x≤5时,﹣x2+5x=6,
∴x1=2(舍),x2=3,
∴P(3,6),
Ⅱ、当x<0,或x>5时,x2﹣5x=6,
∴x3=﹣1,x4=6,
∴P(﹣1,2)或P(6,9),(舍)
即:点P的坐标为(3,6)
(2)解:∵点P(x,y)为直线AB上的一个动点,
∴P(x,x+3),
∴点P到x轴的距离为|x+3|,到y轴的距离为|x|,
∵点B(0,3),
∴BP= ![]() |x|,
|x|,
∵以PB为直径的圆能与坐标轴相切,
∴①以PB为直径的圆能与y轴相切,
∴|x|= ![]() |x|,
|x|,
∴x=0(舍),
②以PB为直径的圆能与x轴相切,
∴|x+3|= ![]() |x|,
|x|,
∴x=﹣6﹣3 ![]() 或x=﹣6+3
或x=﹣6+3 ![]() ,
,
∴P(﹣6﹣3 ![]() ,﹣3+3
,﹣3+3 ![]() )或P(﹣6﹣3
)或P(﹣6﹣3 ![]() ,﹣3﹣3
,﹣3﹣3 ![]() ).
).
故存在点P,坐标为P(﹣6+3 ![]() ,﹣3+3
,﹣3+3 ![]() )或P(﹣6﹣3
)或P(﹣6﹣3 ![]() ,﹣3﹣3
,﹣3﹣3 ![]() )时,以PB为直径的圆能与坐标轴相切
)时,以PB为直径的圆能与坐标轴相切
【解析】(1)易由点A的坐标为(5,8)可得直线AB解析式为y=x+3;从而求得B(0,3),结合对称轴直线x=2,可利用顶点式求得抛物线解析式,顶点C为(2,﹣1)。①从而PE的长为两个函数的差PE=x+3﹣(x2﹣4x+3)=﹣x2+5x,(0≤x≤5)②易得直线AB与这个二次函数图象的对称轴的交点为D,点D坐标易得为(2,5),由四边形DCEP是平行四边形,PE=DC=6,由①中的函数解析式可得当0≤x≤5时,﹣x2+5x=6;当x<0,或x>5时,x2﹣5x=6计算得到点P的坐标为(3,6)
(2)由点P(x,y)为直线AB上的一个动点,可得P(x,x+3)所以点P到x轴的距离为|x+3|,到y轴的距离为|x|,由点B可得BP的长,可判断能与坐标轴相切;分类讨论与x轴或Y轴两种情况,可得最后结果及P取何值时可相切。


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB. 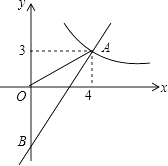
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )

A. 110° B. 120° C. 130° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.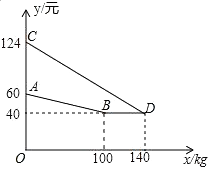
(1)请解释图中点D的实际意义.
(2)求线段CD所表示的y2与x之间的函数表达式.
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
我们知道:一条线段有两个端点,线段![]() 和线段
和线段![]() 表示同一条线段. 若在直线
表示同一条线段. 若在直线![]() 上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了
上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了![]() 个不同的点,共有线段条.(用含
个不同的点,共有线段条.(用含![]() 的代数式表示)
的代数式表示)
类比探究:
以一个锐角的顶点为端点向这个角的内部引射线.
(1)若引出两条射线,则所得图形中共有 个锐角;
(2)若引出![]() 条射线,则所得图形中共有 个锐角.(用含
条射线,则所得图形中共有 个锐角.(用含![]() 的代数式表示)
的代数式表示)
拓展应用:
一条铁路上共有8个火车站,若一列火车往返过程中必须停靠每个车站,则铁路局需为这条线路准备多少种车票?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个箱子里放有1个白球和2个红球,它们除颜色外其余都相同.
(1)判断下列甲乙两人的说法,认为对的在后面括号内答“√”,错的打“×”.
甲:“从箱子里摸出一个球是白球或者红球”这一事件是必然事件;
乙:从箱子里摸出一个球,记下颜色后放回,搅匀,这样连续操作三次,其中必有一次摸到的是白球;
(2)小明说:从箱子里摸出一个球,不放回,再摸出一个球,则“摸出的球中有白球”这一事件的概率为 ![]() ,你认同吗?请画树状图或列表计算说明.
,你认同吗?请画树状图或列表计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
(1)在图中标出点D,并画出该四边形的另两条边;
(2)将四边形ABCD向下平移5个单位,画出平移后得到的四边形A1B1C1D1,并在对称轴AC上找出一点P,使PD+PD1的值最小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com