Question

【题目】某厂家生产并销售某种产品，假设销售量与产量相等，如图中的折线ABD，线段CD分别表示该产品每千克生产成本y1（单位：元），销售价y2（单位：元）与产量x（单位：kg）之间的函数关系．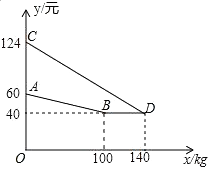

（1）请解释图中点D的实际意义．
（2）求线段CD所表示的y2与x之间的函数表达式．
（3）当该产品产量为多少时，获得的利润最大？最大利润是多少？

Answer 1

【答案】
（1）解：点D的实际意义：当产量为140kg时，该产品每千克生产成本与销售价相等，都为40元

（2）解：设线段CD所表示的y2与x之间的函数表达式为y2=k1x+b1，

∵点（0，124），（140，40）在函数y2=k1x+b1的图象上

∴ ，解得： ，

∴y2与x之间的函数表达式为y2=﹣ x+124（0≤x≤140）

（3）解：设线段AB所表示的y1与x之间的函数表达式为y1=k2x+b2，

∵点（0，60），（100，40）在函数y1=k2x+b2的图象上

∴ ，解得： ，

∴y1与x之间的函数表达式为y1=﹣ x+60（0≤x≤100）

设产量为x千克时，获得的利润为W元

①当0≤x≤100时，W=[（﹣ x+124）﹣（﹣ x+60）]x=﹣ （x﹣80）2+2560，

∴当x=80时，W的值最大，最大值为2560元．

②当100≤x≤140时，W=[（﹣ x+124）﹣40]x=﹣ （x﹣70）2+2940

由﹣ ＜0知，当x≥70时，W随x的增大而减小

∴当x=100时，W的值最大，最大值为2400元．

∵2560＞2400，

∴当该产品的质量为80kg时，获得的利润最大，最大利润为2560元

【解析】（1）交点D为x取相同数时y1=y2所以易得点D的实际意义。
（2）已知点C，点D坐标，所以易由待定系数法求得直线CD的解析式。
（3）由于销售量与产量的函数图像分为两段，所以需要分情况讨论，而我们的利润是（售价-成本）×数量，所以结合（2）中的解析式可得利润的解析式分别为①当0≤x≤100时W==﹣ （x﹣80）2+2560②当100≤x≤140时，W=﹣ （x﹣70）2+2940，结合两个函数的最值，可得结果。
【考点精析】关于本题考查的二次函数的性质和二次函数的最值，需要了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a才能得出正确答案．