
【题目】经过三角形一边的中点,画另一边的平行线,则这条平行线平分第三边;三角形两边中点之间线段的长度等于第三边长度的一半.
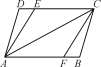
如图,要判定AB∥CD,需要哪些条件?根据是什么?
【答案】见解析.
【解析】
利用平行线判定定理,内错角相等,两直线平行;同旁内角互补,两直线平行;同位角相等,两直线平行即可解题.
①若考虑截线AD,则需∠D+∠DAB=180°,根据是同旁内角互补,两直线平行.
②若考虑截线AE,则需∠CEA+∠EAB=180°,根据是同旁内角互补,两直线平行或∠DEA=∠EAB,根据是内错角相等,两直线平行.
③若考虑截线AC,则需∠DCA=∠CAB,根据是内错角相等,两直线平行.
④若考虑截线FC,则需∠DCF+∠AFC=180°,根据是同旁内角互补,两直线平行或∠DCF=∠BFC,根据是内错角相等,两直线平行.
⑤若考虑截线BC,则需∠DCB+∠B=180°,根据是同旁内角互补,两直线平行.


科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示,先将△ABC向右平移3个单位,再向下平移1个单位到△A1B1C1,△A1B1C1和△A2B2C2关于x轴对称

(1)画出△A1B1C1和△A2B2C2
(2)在x轴上确定一点P,使BP+A1P的值最小,直接写出P的坐标为________
(3)点Q在坐标轴上且满足△ACQ为等腰三角形,则这样的Q点有 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,点A、点B均为格点.
(1)AB的长等于;
(2)若点C是以AB为底边的等腰直角三角形的顶点,点D在边AC上,且满足S△ABD= ![]() S△ABC . 请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置时如何找到的(不要求证明). .
S△ABC . 请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置时如何找到的(不要求证明). .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小华做观察水的沸腾实验时所记录的数据:

(1)时间是8分钟时,水的温度为_____;
(2)此表反映了变量_____和_____之间的关系,其中_____是自变量,_____是因变量;
(3)在_____时间内,温度随时间增加而增加;_____时间内,水的温度不再变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时生产同一种零件,在10天中两台机床每天生产的次品数如下:
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
(1)分别计算两组数据的平均数和方差;
(2)从结果看,在10天中哪台机床出现次品的波动较小?
(3)由此推测哪台机床的性能较好
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB. 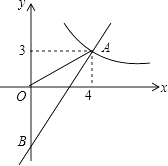
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案1:所有评委所给分的平均数,
方案2:在所有评委所给分中,去掉一个最高分和一个最低分.然后再计算其余给分的l平均数.
方案3:所有评委所给分的中位效.
方案4:所有评委所给分的众数.
为了探究上述方案的合理性.先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适台作为这个同学演讲的最后得分,并给出该同学的最后得分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.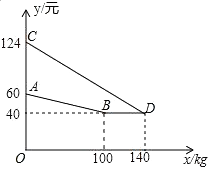
(1)请解释图中点D的实际意义.
(2)求线段CD所表示的y2与x之间的函数表达式.
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com