
【题目】如图,自来水厂A和村庄B在小河PQ的两侧,现要在A,B间铺设一条输水管道,为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行2.4km,到达点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.
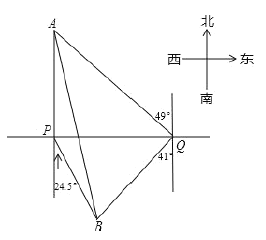
(1)求BQ长度;
(2)求A、B间的距离(参考数据![]() ).
).
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)首先由已知求出∠PBQ和∠BPQ的度数,可知两角相等,于是得出线段BQ与PQ相等,即可求解;
(2)先由已知求出∠PQA,再由直角三角形PQA求出AQ,又由已知得∠AQB=90°,所以根据勾股定理求出A,B间的距离.
解:(1)∵∠PQB=90°-41°=49°,∠BPQ=90°-24.5°=65.5°,
∴∠PBQ=180°-49°-65.5°=65.5°,
∴∠BPQ=∠PBQ,
∴BQ=PQ=2.4(km);
(2)∠AQB=180°-49°-41°=90°,∠PQA=90°-49°=41°,
∴AQ= ![]() (km),
(km),
∵BQ=PQ=2.4,
∴AB2=AQ2+BQ2=3.22+2.42=16,
∴AB=4,
答:A、B的距离为4 km.


科目:初中数学 来源: 题型:
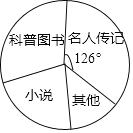
【题目】2018年东营市教育局在全市中小学开展了“情系疏勒书香援疆”捐书活动,200多所学校的师生踊跃参与,向新疆疏勒县中小学共捐赠爱心图书28.5万余本.某学校学生社团对本校九年级学生所捐图书进行统计,根据收集的数据绘制了下面不完整的统计图表.请你根据统计图表中所提供的信息解答下列问题:
图书种类 | 频数(本) | 频率 |
名人传记 | 175 | a |
科普图书 | b | 0.30 |
小说 | 110 | c |
其他 | 65 | d |
(1)求该校九年级共捐书多少本;
(2)统计表中的a= ,b= ,c= ,d= ;
(3)若该校共捐书1500本,请估计“科普图书”和“小说”一共多少本;
(4)该社团3名成员各捐书1本,分别是1本“名人传记”,1本“科普图书”,1本“小说”,要从这3人中任选2人为受赠者写一份自己所捐图书的简介,请用列表法或树状图求选出的2人恰好1人捐“名人传记”,1人捐“科普图书”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
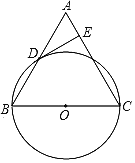
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为10,tanB=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,tan∠ACB=![]() ,将其沿对角线AC剪开得到△ABC和△ADE(点C与点E重合),将△ADE绕点A旋转,当线段AD与AB在同一条直线上时,连接EC,则∠ECB的正切值为_____.
,将其沿对角线AC剪开得到△ABC和△ADE(点C与点E重合),将△ADE绕点A旋转,当线段AD与AB在同一条直线上时,连接EC,则∠ECB的正切值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
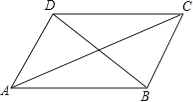
A.①②B.②③C.①③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
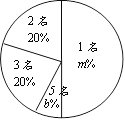
【题目】为了有效地落实国家精准扶贫政策,切实关爱贫困家庭学生.某校对全校各班贫困家庭学生的人数情况进行了调查.发现每个班级都有贫困家庭学生,经统计班上贫困家庭学生人数分别有1名、2名、3名、5名,共四种情况,并将其制成了如下两幅不完整的统计图:
(1)填空:a = ,b= ;
(2)求这所学校平均每班贫困学生人数;
(3)某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表或画树状图的方法,求出被选中的两名学生来自同一班级的概率.
贫困学生人数 | 班级数 |
1名 | 5 |
2名 | 2 |
3名 | a |
5名 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
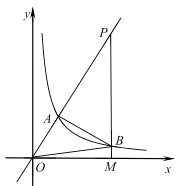
【题目】如图,反比例函数![]() 的图象与正比例函数
的图象与正比例函数![]() 图象交于点
图象交于点![]() ,且点
,且点![]() 的横坐标为2.
的横坐标为2.
(1)求反比例函数的表达式;
(2)若射线![]() 上有一点
上有一点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 与
与![]() 轴垂直,垂足为
轴垂直,垂足为![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() ,
,![]() ,请求出
,请求出![]() 的面积.
的面积.
(3)定义:横纵坐标均为整数的点称为“整点”.在(2)的条件下,请探究边![]() ,
,![]() 与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝新中国成立七十周年,某校开展了“祖国在我心中”手抄报展评活动.小红同学设计的手抄报如右图所示,手抄报的外边框长![]() ,宽
,宽![]() ,正中央是一个与整个手抄报长宽比例相同的矩形.又知四周边衬所占面积是手抄报面积的四分之一,上、下边衬等宽,左、右边衬等宽,求小红设计手抄报的四周边衬的宽度. (精确到
,正中央是一个与整个手抄报长宽比例相同的矩形.又知四周边衬所占面积是手抄报面积的四分之一,上、下边衬等宽,左、右边衬等宽,求小红设计手抄报的四周边衬的宽度. (精确到![]() )
)
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c与x轴交于点A(4,﹣5).
(1)如图,过点A分别向x轴、y轴作垂线,垂足分别为B、C,得到矩形ABOC,且抛物线经过点C.
①求抛物线的解析式.
②将抛物线沿直线x=m(2>m>0)翻折,分别交线段OB、AC于D,E两点.若直线DE刚好平分矩形ABOC的面积,求m的值.
(2)将抛物线旋转180°,使点A的对应点为A1(m﹣2,n﹣4),其中m≤2.若旋转后的抛物线仍然经过点A,求旋转后的抛物线顶点所能达到最低点时的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com