
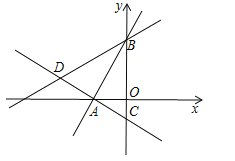
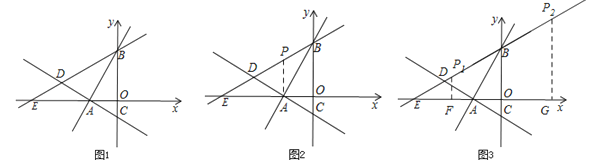
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�����A��![]() ��0��������ֱ�߷ֱ�y����B��C���㣬��B��C�����������ֱ���һԪ���η���
��0��������ֱ�߷ֱ�y����B��C���㣬��B��C�����������ֱ���һԪ���η���![]() ����������
����������
��1�����߶�BC�ij��ȣ�
��2�����ʣ�ֱ��AC��ֱ��AB�Ƿ�ֱ����˵�����ɣ�
��3������D��ֱ��AC�ϣ���DB=DC�����D�����ꣻ
��4���ڣ�3���������£�ֱ��BD���Ƿ���ڵ�P��ʹ��A��B��P����Ϊ������������ǵ��������Σ������ڣ���ֱ��д��P������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��4����2����ֱ����3��D��![]() ��1������4��P��
��1������4��P��![]() ��0������
��0������![]() ��2��������3��
��2��������3��![]() ������3��
������3��![]() ����
����
��������
�����������1����![]() ����x=3��x=��1����B��0��3����C��0����1������BC=4��
����x=3��x=��1����B��0��3����C��0����1������BC=4��
��2����A��![]() ��0����B��0��3����C��0����1������OA=
��0����B��0��3����C��0����1������OA=![]() ��OB=3��OC=1����
��OB=3��OC=1����![]() =OBOC������AOC=��BOA=90�㣬����AOC�ס�BOA������CAO=��ABO������CAO+��BAO=��ABO+��BAO=90�㣬����BAC=90�㣬��AC��AB��
=OBOC������AOC=��BOA=90�㣬����AOC�ס�BOA������CAO=��ABO������CAO+��BAO=��ABO+��BAO=90�㣬����BAC=90�㣬��AC��AB��
��3����ֱ��AC�Ľ���ʽΪy=kx+b����A��![]() ��0����C��0����1������y=kx+b����
��0����C��0����1������y=kx+b����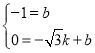 ����ã�
����ã�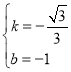 ����ֱ��AC�Ľ���ʽΪ��
����ֱ��AC�Ľ���ʽΪ��![]() ����DB=DC������D���߶�BC�Ĵ�ֱƽ�����ϣ���D��������Ϊ1������y=1����
����DB=DC������D���߶�BC�Ĵ�ֱƽ�����ϣ���D��������Ϊ1������y=1����![]() ����x=
����x=![]() ����D��������
����D��������![]() ��1����
��1����
��4����ֱ��BD�Ľ���ʽΪ��y=mx+n��ֱ��BD��x�ύ�ڵ�E����B��0��3����D��![]() ��1������y=mx+n����
��1������y=mx+n����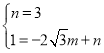 �������
������� ����ֱ��BD�Ľ���ʽΪ��
����ֱ��BD�Ľ���ʽΪ��![]() ����y=0����
����y=0����![]() ����x=
����x=![]() ����E��
����E��![]() ��0������OE=
��0������OE=![]() ����tan��BEC=
����tan��BEC=![]() =
=![]() ������BEO=30�㣬ͬ������ã���ABO=30�㣬����ABE=30����
������BEO=30�㣬ͬ������ã���ABO=30�㣬����ABE=30����
��PA=ABʱ����ͼ1����ʱ����BEA=��ABE=30�㣬��EA=AB����P��E�غϣ���P������Ϊ��![]() ��0������PA=PBʱ����ͼ2����ʱ����PAB=��PBA=30�㣬����ABE=��ABO=30�㣬����PAB=��ABO����PA��BC������PAO=90�㣬����P�ĺ�����Ϊ
��0������PA=PBʱ����ͼ2����ʱ����PAB=��PBA=30�㣬����ABE=��ABO=30�㣬����PAB=��ABO����PA��BC������PAO=90�㣬����P�ĺ�����Ϊ![]() ����x=
����x=![]() ����
����![]() ����y=2����P��
����y=2����P��![]() ��2����
��2����
��PB=ABʱ����ͼ3�����ɹ��ɶ�������ã�AB=![]() ��EB=6������P��y�����ʱ���Ǵ�ʱ��PΪP1������P1��P1F��x���ڵ�F����P1B=AB=
��EB=6������P��y�����ʱ���Ǵ�ʱ��PΪP1������P1��P1F��x���ڵ�F����P1B=AB=![]() ����EP1=6��
����EP1=6��![]() ����sin��BEO=
����sin��BEO=![]() ����FP1=
����FP1=![]() ����y=
����y=![]() ����
����![]() ����x=��3����P1����3��
����x=��3����P1����3��![]() ��������P��y����Ҳ�ʱ���Ǵ�ʱ��PΪP2������P2��P2G��x���ڵ�G����P2B=AB=
��������P��y����Ҳ�ʱ���Ǵ�ʱ��PΪP2������P2��P2G��x���ڵ�G����P2B=AB=![]() ����EP2=6+
����EP2=6+![]() ����sin��BEO=
����sin��BEO=![]() ����GP2=
����GP2=![]() ����y=
����y=![]() ����
����![]() ����x=3����P2��3��
����x=3����P2��3��![]() ����
����
������������A��B��P����Ϊ������������ǵ���������ʱ����P������Ϊ��![]() ��0������
��0������![]() ��2��������3��
��2��������3��![]() ������3��
������3��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ԥ���½������Ὣ����Լ69 000 000�˴βιۣ���69 000 000�ÿ�ѧ��������ʾ��ȷ���ǣ� ��
A.0.69��108
B.6.9��106
C.6.9��107
D.69��106
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ����ѧ������Զ���п�����������ȡ������ijɼ����ڶ���һ���º�ѧУ�Ծ��꼶һ���45��ѧ�����в��ԣ��ɼ����±���
��Զ�ɼ���cm�� | 160 | 170 | 180 | 190 | 200 | 220 |
���� | 3 | 9 | 6 | 9 | 15 | 3 |
��Щ�˶�Ա��Զ�ɼ�����λ���������ֱ��ǣ� ��
A.190��200
B.9��9
C.15��9
D.185��200
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�ڡ�ABC����ADE�У���BAC=��DAE=90�㣬AB=AC��AD=AE����C��D��E������ͬһ��ֱ���ϣ�����BD��BE�������ĸ����ۣ���BD=CE����BD��CE���ۡ�ACE+��DBC=45�㣻��BE2=2��AD2+AB2����CD2 �� ���н�����ȷ�ĸ����ǣ� �� 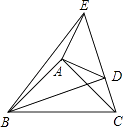
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
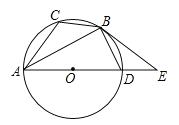
����Ŀ����ͼ����֪��O�ǡ�ABC�����Բ��AD�ǡ�O��ֱ������BD=BC���ӳ�AD��E�����С�EBD=��CAB��
��1����֤��BE�ǡ�O�����ߣ�
��2����BC=![]() ��AC=5����Բ��ֱ��AD������BE�ij���
��AC=5����Բ��ֱ��AD������BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���غӰ���A��B��C�����ۿڣ��ס�������ͬʱ�ֱ��A��B�ۿڳ���������ʻ��C�ۣ����յ���C�ۣ���ס���������ʻx��h������B�۵ľ���ֱ�Ϊy1��y2��km����y1��y2��x�ĺ�����ϵ��ͼ��ʾ���������н��ۣ�
�ټ״����ٶ���25km/h��
�ڴ�A�۵�C��ȫ��Ϊ120km��
�ۼ״����Ҵ���1.5Сʱ�����յ㣻
��ͼ��P��Ϊ���������Ľ��㣬P�������Ϊ�� ![]() ����
����
������������С��10km�ܹ����������ô���ס����������������ʱ��x��ȡֵ��Χ�� ![]() ��x��2��
��x��2��
������ȷ�Ľ����� �� 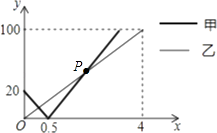
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����x����Ϸ���ֱ�ǡ�BOA��ԭ��O��˳ʱ�뷽����ת������BOA�����߷ֱ��뺯��![]() ��
��![]() ��ͼ����B��A���㣬���OAB�Ĵ�С�ı仯����Ϊ�� ��
��ͼ����B��A���㣬���OAB�Ĵ�С�ı仯����Ϊ�� ��

A����С B����� C��ʱ��ʱС D�����ֲ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com