
【题目】已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)﹣CD2 , 其中结论正确的个数是( ) 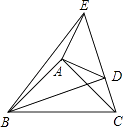
A.1
B.2
C.3
D.4
【答案】D
【解析】解:如图: ①∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE.
在△ABD和△ACE中,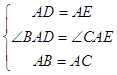 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∴①正确;
②∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ABD+∠DBC=45°.
∴∠ACE+∠DBC=45°,∴③正确;
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵∠CAB=90°,
∴∠ABD+∠AFB=90°,
∴∠ACE+∠AFB=90°.
∵∠DFC=∠AFB,
∴∠ACE+∠DFC=90°,
∴∠FDC=90°.
∴BD⊥CE,∴②正确;
④∵BD⊥CE,
∴BE2=BD2+DE2 ,
∵∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴DE2=2AD2 , BC2=2AB2 ,
∵BC2=BD2+CD2 ,
∴2AB2=BD2+CD2 ,
∴BD2=2AB2﹣CD2 ,
∴BE2=BD2+DE2=2AB2﹣CD2+2AD2=2(AD2+AB2)﹣CD2 ,
∴④正确.
故选D.
①由条件证明△ABD≌△ACE,就可以得到结论;
②由条件知∠ABC=∠ABD+∠DBC=45°,由∠ABD=∠ACE就可以得出结论;
③由△ABD≌△ACE就可以得出∠ABD=∠ACE,就可以得出∠BDC=90°,进而得出结论;
④△BDE为直角三角形就可以得出BE2=BD2+DE2 , 由△DAE和△BAC是等腰直角三角形就有DE2=2AD2 , BC2=2AB2 , 就有BC2=BD2+CD2就可以得出结论.


科目:初中数学 来源: 题型:
【题目】已知点P(![]() ,
,![]() )和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=
)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=![]() =
=![]() =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线![]() 的位置关系并说明理由;
的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了绿化环境,育英中学八年级三班同学都积极参加植树活动,今年植树节时,该班同学植树情况的部分数据如图所示,请根据统计图信息,回答下列问题:(第(1),(3)小题需列式解答)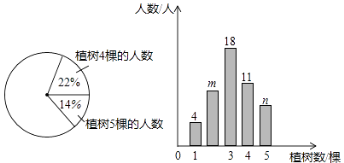
(1)八牛级三班共有多少名同学?
(2)条形统计图中,m= , n=。
(3)扇形统计图中,算出植树2棵的人数所对应的扇形圆心角的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在开展“学雷锋社会实践”活动中,某校为了解全校1200名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成条形统计图如图. 
(Ⅰ)求这50个样本数据的平均数、众数和中位数;
(Ⅱ)根据样本数据,估算该校1200名学生共参加了多少次活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点, 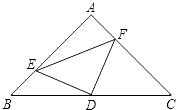
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
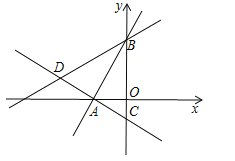
【题目】如图所示,在平面直角坐标系中,过点A(![]() ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程![]() 的两个根.
的两个根.
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标;
(4)在(3)的条件下,直线BD上是否存在点P,使以A、B、P三点为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,无限循环小数都可以转化为分数.例如:将 ![]() 转化为分数时,可设
转化为分数时,可设 ![]() =x,则x=0.3+
=x,则x=0.3+ ![]() x,解得x=
x,解得x= ![]() ,即
,即 ![]() =
= ![]() .仿此方法,将
.仿此方法,将 ![]() 化成分数是 .
化成分数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E. 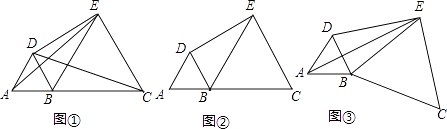
(1)如图①,连结CD,AE,求证:CD=AE;
(2)如图②,若AB=1,BC=2,求DE的长;
(3)如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2 , 试求∠DEB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com