
【题目】已知关于 ![]() 的方程
的方程 ![]() 有两个实数根
有两个实数根 ![]() 、
、 ![]() .
.
(1)求实数k的取值范围;
(2)若 ![]() 、
、 ![]() 满足
满足 ![]() ,求实数
,求实数 ![]() 的值.
的值.
【答案】
(1)解:∵关于x的方程x2+(2k﹣1)x+k2﹣1=0有两个实数根x1 , x2 ,
∴△=(2k﹣1)2﹣4(k2﹣1)=﹣4k+5≥0,
解得:k≤ ![]() ,
,
∴实数k的取值范围为k≤ ![]()
(2)解:∵关于x的方程x2+(2k﹣1)x+k2﹣1=0有两个实数根x1 , x2 ,
∴x1+x2=1﹣2k,x1x2=k2﹣1,
∵x12+x22=(x1+x2)2﹣2x1x2=16+x1x2 ,
∴(1﹣2k)2﹣2×(k2﹣1)=16+(k2﹣1),即k2﹣4k﹣12=0,
解得:k=﹣2或k=6(不符合题意,舍去),
∴实数k的值为﹣2
【解析】(1)根据一元二次方程的定义和根的判别式的意义得到k2≠0且△=4(k+1)2-4k2≥0,然后解两个不等式,求出它们的公共部分即可;
(2)先把k=1代入方程,再根据根与系数的关系得到x1+x2=4,x1x2=1,然后把所求的代数式变形,然后利用整体思想进行计算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求S△COB .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD、AE分别是Rt△ABC的高和中线,AB=9cm,AC=12cm,BC=15cm,试求:
(1)AD的长度;
(2)△ACE和△ABE的周长的差.
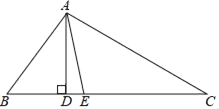
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y= ![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )

A.AB=CDB.AB∥CDC.∠A=∠CD.BC=AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com