
【题目】如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求S△COB .
【答案】
(1)解:设直线表达式为y=kx+b.
∵A(2,0),B(1,1)都在y=kx+b的图象上,
∴ ![]() ,解得
,解得 ![]() ,
,
∴直线AB的表达式为y=﹣x+2;
∵点B(1,1)在y=ax2的图象上,
∴a=1,其表达式为y=x2
(2)解:由 ![]() ,解得
,解得 ![]() 或
或 ![]() ,
,
∴点C坐标为(﹣2,4)
(3)解:S△COB=S△AOC﹣S△OAB= ![]() ×2×4﹣
×2×4﹣ ![]() ×2×1=3
×2×1=3
【解析】已知直线AB经过A(2,0),B(1,1),设直线表达式为y=kx+b,可求直线解析式;将B(1,1)代入抛物线y=ax2可求抛物线解析式;
将第一小题中所求的直线AB的解析式与抛物线y=ax2的解析式联立,得到方程组,解方程即可求出点C的坐标;
已知A,B,C三点坐标,根据S△COB=S△AOC-S△OAB即可求△COB的面积.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】某工厂新开发生产一种机器,每台机器成本y(万元)与生产数量x(台)之间满足一次函数关系(其中10≤x≤70,且为整数),函数y与自变量x的部分对应值如表
| 10 | 20 | 30 |
| 60 | 55 | 50 |
(1)求y与x之间的函数关系式;

(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.则当该厂第一个月生产的这种机器40台都按同一售价全部售出,请求出该厂第一个月销售这种机器的总利润.(注:利润=售价﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)11![]() -1
-1![]() -1
-1![]() +4
+4![]() ;
;
(2)(-22.84)-(+38.57)+(-37.16)-(-32.57);
(3)1![]() -
-![]() +2
+2![]() +
+![]() -4
-4![]() ;
;
(4)(-36)-(-28)+(+125)+(-4)-(+53)-(-40).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上以每秒
边上以每秒![]() 的速度从点
的速度从点![]() 向点
向点![]() 运动,点
运动,点![]() 在
在![]() 边上,以每秒
边上,以每秒![]() 的速度从点
的速度从点![]() 出发,在
出发,在![]() 间往返运动,两个点同时出发,当点
间往返运动,两个点同时出发,当点![]() 到达点
到达点![]() 时停止(同时点
时停止(同时点![]() 也停止).设运动时间为
也停止).设运动时间为![]() 秒,当
秒,当![]() 为何值时,以点
为何值时,以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?
为顶点的四边形是平行四边形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )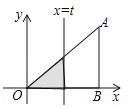
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中折线表示芳芳骑自行车离家的距离与时间的关系,她9点离开家,15点回家,请根据图象回答下列问题:

(1)芳芳到达离家最远的地方时,离家________千米;
(2)第一次休息时离家________ 千米;
(3)她在10:00~10:30的平均速度是_________;
(4)芳芳一共休息了_________ 小时;
(5)芳芳返回用了____________小时;
(6)返回时的平均速度是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在⊙O中. AE直径,AD是弦,B为AE延长线上--点,作BC⊥AD,与AD延长线交于点C.且∠CBD=∠A.
(1)判断直线BD与⊙0的位置关系,并证明你的结论;
(2)若∠A=30 ![]() ,OA=6,求图中阴影部分的面积.
,OA=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为给研究制定《中考改革实施方案》提出合理化建议,教研人员对九年级学生进行了随机抽样调查,要求被抽查的学生从物理、化学、政治、历史、生物和地理这六个选考科目中,挑选出一科作为自己的首选科目,将调查数据汇总整理后,绘制出了如图的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生共有多少人?
(2)将折线统计图补充完整;
(3)我市现有九年级学生约40000人,请你估计首选科目是物理的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com