Question

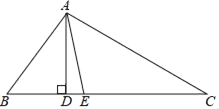
【题目】如图，已知AD、AE分别是Rt△ABC的高和中线，AB＝9cm，AC＝12cm，BC＝15cm，试求：

（1）AD的长度；

（2）△ACE和△ABE的周长的差．

Answer 1

【答案】（1）AD的长度为cm；（2）△ACE和△ABE的周长的差是3cm．

【解析】

（1）利用直角三角形的面积法来求线段AD的长度；

（2）由于AE是中线，那么BE＝CE，再表示△ACE的周长和△ABE的周长，化简可得△ACE的周长﹣△ABE的周长＝AC﹣AB即可．

解：（1）∵∠BAC＝90°，AD是边BC上的高，

∴S△ACB=ABAC＝BCAD，

∵AB＝9cm，AC＝12cm，BC＝15cm，

∴AD＝＝＝（cm），

即AD的长度为cm；

（2）∵AE为BC边上的中线，

∴BE＝CE，

∴△ACE的周长﹣△ABE的周长＝AC+AE+CE﹣（AB+BE+AE）＝AC﹣AB＝12﹣9＝3（cm），

即△ACE和△ABE的周长的差是3cm．