
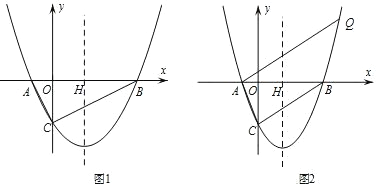
【题目】已知,抛物线 y=![]() x2+bx+c 与 y 轴交于点 C,与 x 轴交于点 A 和点B(其中点 A 在 y 轴左侧,点 B 在 y 轴右侧),对称轴直线 x=
x2+bx+c 与 y 轴交于点 C,与 x 轴交于点 A 和点B(其中点 A 在 y 轴左侧,点 B 在 y 轴右侧),对称轴直线 x=![]() 交 x 轴于点 H.
交 x 轴于点 H.
(1)若抛物线y=![]() x2+bx+c经过点(﹣4,6),求抛物线的解析式;
x2+bx+c经过点(﹣4,6),求抛物线的解析式;
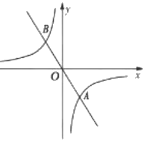
(2)如图1,∠ACB=90°,点P是抛物线y=![]() x2+bx+c上位于y轴右侧的动点,且 S△ABP=S△ABC,求点 P 的坐标;
x2+bx+c上位于y轴右侧的动点,且 S△ABP=S△ABC,求点 P 的坐标;
(3)如图 2,过点A作AQ∥BC交抛物线于点Q,若点Q的纵坐标为﹣![]() c, 求点Q的坐标.
c, 求点Q的坐标.
【答案】(1)y=![]() x2-
x2-![]() x-8;(2)点 P 的坐标为(3,﹣2),(
x-8;(2)点 P 的坐标为(3,﹣2),(![]() ,2);(3)点 Q 的坐标是(7,9).
,2);(3)点 Q 的坐标是(7,9).
【解析】
(1)根据对称轴和点的坐标即可求出函数的解析式;
(2)连接 CH,利用交点式和韦达定理求出CH2及AB2
, 在 Rt△OHC 中,由勾股定理求出c的值,再分情况讨论即可.
(3)分别利用直线 BC和直线AC联系二次函数解析式消去y得到两个含k,c的方程,即可解出k,c的值,得出Q点坐标.
(1)∵抛物线 y=![]() x2+bx+c 的对称轴是直线 x=
x2+bx+c 的对称轴是直线 x=![]() ,
,
∴﹣![]() =﹣b=
=﹣b=![]() ,
,
∴b=﹣![]() .
.
又抛物线 y=![]() x2+bx+c 经过点(﹣4,6),
x2+bx+c 经过点(﹣4,6),
∴6=![]() ×(﹣4)2﹣
×(﹣4)2﹣![]() ×(﹣4)+c, 解得 c=﹣8.
×(﹣4)+c, 解得 c=﹣8.
故该抛物线解析式是 y =![]() x2﹣
x2﹣![]() x﹣8;
x﹣8;
如图 1,连接 CH,
∵对称轴直线 x=![]() 交 x 轴于点 H,
交 x 轴于点 H,
∴AH=BH,OH=![]() . 又∵∠ACB=90°,
. 又∵∠ACB=90°,
∴CH= ![]() AB,
AB,
设 A,B 两点的坐标分别为(x1,0),(x2,0),
则 x1,x2 是方程![]() x2﹣
x2﹣![]() x+c=0 的两根,
x+c=0 的两根,
∴x1+x2=3,x1x2=2c,
∴AB2=(x2﹣x1)2=(x1+x2)2﹣4x1x2=9﹣8c,
∴CH2=![]() AB2=
AB2=![]() ﹣2c.
﹣2c.
在 Rt△OHC 中,由勾股定理得:CH2=OH2+OC2,即:c2+2c=0, 解得:c=﹣2 或 c=0(舍去).
∵S△ABP=S△ABC,
∴|yP|=|yC|=2.
①当 yP=﹣2 时,点 P 与点 C 关于直线 x=![]() 对称,
对称,
∴P(3,﹣2).
②当 yP=2 时,![]() x2﹣
x2﹣![]() x﹣2=2, 解得:x=
x﹣2=2, 解得:x=![]() .
.
又∵点 P 在 y 轴的右侧,
∴x= ![]() ,
,
∴点 P 的坐标为( ![]() ,2).综上所述,符合条件的点 P 的坐标为(3,﹣2),(
,2).综上所述,符合条件的点 P 的坐标为(3,﹣2),(![]() ,2).
,2).
如图 2,设直线 BC 的解析式为:y=kx+c(k≠0),联立直线 BC 与抛物线的解析式,得 ,
,
消去 y,得![]() x2﹣
x2﹣![]() x+c=kx+c, 解得:xC=0,xB=3+2k,
x+c=kx+c, 解得:xC=0,xB=3+2k,
由(2)知 xA+xB=3,
∴xA=3﹣xB,
∴xA=﹣2k.
把点 B 的坐标(3+2k,0)代入 y=kx+c,得 c=﹣k(3+2k)=﹣3k﹣2k2.
∵AQ∥BC,
则设 AQ 的解析式为:y=kx+m(k≠0).联立直线 AQ 与抛物线的解析式,得
消去 y,得![]() x2﹣
x2﹣ ![]() x+c=kx+m,
x+c=kx+m,
设点 A、Q 的横坐标分别为 xA、xQ, 则 xA+xQ=3+2k,
∵xA=﹣2k,
∴xQ=3+4k.
又∵yQ=﹣ ![]() c,c=﹣3k﹣2k2.
c,c=﹣3k﹣2k2.
则有:﹣![]() (﹣3k﹣2k2)=
(﹣3k﹣2k2)=![]() (3+4k)2﹣
(3+4k)2﹣![]() (3+4k)+(﹣3k﹣2k2),解得:k1=0(舍去),k2=1,
(3+4k)+(﹣3k﹣2k2),解得:k1=0(舍去),k2=1,
∴c=﹣3k﹣2k2=﹣5,
∴点 Q 的坐标是(7,9).


科目:初中数学 来源: 题型:
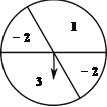
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
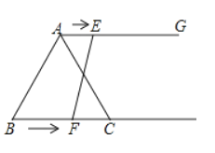
【题目】如图,在等边![]() 中,
中,![]() ,射线
,射线![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,如果点
的速度运动,如果点![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() ,当
,当![]() 时,以
时,以![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
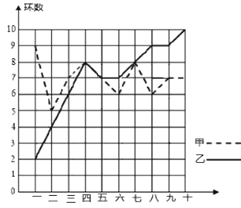
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
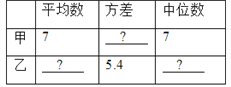
(1)请将下表补充完整:
(2)请从下列三个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c(a≠0)中,函数 y 与自变量 x 的部分对应值如下表:
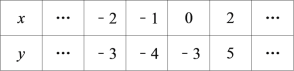
(1)求二次函数的解析式;
(2)求该函数图象与 x 轴的交点坐标;
(3)不等式 ax2+bx+c+3>0 的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弦AB,CD是⊙O的两条平行弦,⊙O的半径为5,AB=8,CD=6,则AB,CD之间的距离为( )
A. 7 B. 1 C. 4或3 D. 7或1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y= -2x和反比例函数![]() 的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线
的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线![]() 交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______
交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB.
小明的做法如下:
如图
①作线段AB的垂直平分线m;
②作线段BC的垂直平分线n,与直线m交于点O;
③以点O为圆心,OA为半径作△ABC的外接圆;
④在弧ACB上取一点P,连结AP,BP.
所以∠APB=∠ACB.
老师说:“小明的作法正确.”
请回答:
(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是_____;
(2)∠APB=∠ACB的依据是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买甲,乙两种型号的垃圾处理设备共10台,已知每台甲型设备日处理能力为12吨,每台乙型设备日处理能力为15吨,购回的设备日处理能力总计不低于140吨.
(1)请你为该景区设计购买甲,乙两种设备的方案;
(2)已知每台甲型设备价格为3万元,每台乙型设备价格为4.4万元.厂家为了促销产品,规定总货款不低于40万元时,可按9折优惠.问采用(1)中设计的哪种购买方案,使购买费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com