
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点.
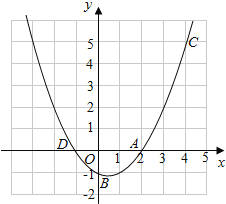
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
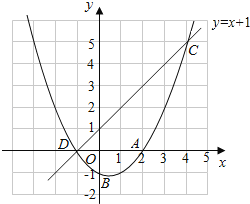
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣1;(2)点D坐标为(﹣1,0);(3)x的取值范围是﹣1<x<4.
x﹣1;(2)点D坐标为(﹣1,0);(3)x的取值范围是﹣1<x<4.
【解析】
试题分析:(1)根据二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点,代入得出关于a,b,c的三元一次方程组,求得a,b,c,从而得出二次函数的解析式;
(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;
(3)画出图象,再根据图象直接得出答案.
解:(1)∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点,
∴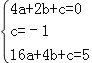 ,
,
∴a=![]() ,b=﹣
,b=﹣![]() ,c=﹣1,
,c=﹣1,
∴二次函数的解析式为y=![]() x2﹣
x2﹣![]() x﹣1;
x﹣1;
(2)当y=0时,得![]() x2﹣
x2﹣![]() x﹣1=0;
x﹣1=0;
解得x1=2,x2=﹣1,
∴点D坐标为(﹣1,0);
(3)图象如图,
当一次函数的值大于二次函数的值时,x的取值范围是﹣1<x<4.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
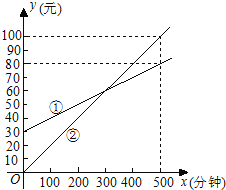
(1)有月租费的收费方式是 (填①或②),月租费是 元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简,求值
(1)5x2y+{xy﹣[5x2y﹣(7xy2+![]() xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣
xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣![]() ,y=﹣16.
,y=﹣16.
(2)A=4x2﹣2xy+4y2,B=3x2﹣6xy+3y2,且|x|=3,y2=16,|x+y|=1,求4A+[(2A﹣B)﹣3(A+B)]的值.
(3)如果m﹣3n+4=0,求:(m﹣3n)2+7m3﹣3(2m3n﹣m2n﹣1)+3(m3+2m3n﹣m2n+n)﹣m﹣10m3的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:在平面直角坐标系中,以点M(0,![]() )为圆心,2
)为圆心,2![]() 为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于点P,连接PC交x轴于点E.
为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于点P,连接PC交x轴于点E.

(1)求点C,P的坐标;
(2)求弓形![]() 的面积;
的面积;
(3)探求线段BE和OE存在何种数量关系,并证明你所得到的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).
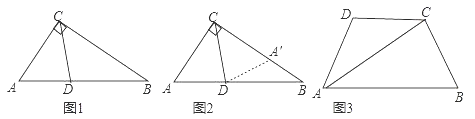
请回答:
(1)在图2中,小明得到的全等三角形是△ ≌△ ;
(2)BC和AC、AD之间的数量关系是 .
参考小明思考问题的方法,解决问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9.求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架2.5米长的梯子,斜靠在一竖直的墙上,这时梯足到墙底端的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?(5分)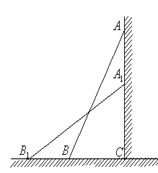
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3个有理数x、y、z,若![]() 且x与y互为相反数,y与z互为倒数.
且x与y互为相反数,y与z互为倒数.
(1)当n为奇数时,你能求出x、y、z这三个数吗?当n为偶数时,你能求出x、y、z这三个数吗?能,请计算并写出结果;不能,请说明理由.
(2)根据(1)的结果计算:xy﹣yn﹣(y﹣z)2011的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com