
【题目】如图所示:在平面直角坐标系中,以点M(0,![]() )为圆心,2
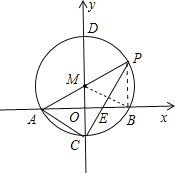
)为圆心,2![]() 为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于点P,连接PC交x轴于点E.
为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于点P,连接PC交x轴于点E.

(1)求点C,P的坐标;
(2)求弓形![]() 的面积;
的面积;
(3)探求线段BE和OE存在何种数量关系,并证明你所得到的结论.
【答案】(1)P点坐标为(3,2![]() ),C(0,﹣
),C(0,﹣![]() );(2)S弓形ACB=4π﹣
);(2)S弓形ACB=4π﹣![]() ;(3)BE=2OE,见解析
;(3)BE=2OE,见解析
【解析】
试题分析:(1)连接PB.根据直径所对的圆周角是直角判定PB⊥OM;由已知条件OA=OB推知OM是三角形APB的中位线;最后根据三角形的中位线定理求得点P的坐标、由⊙M的半径长求得点C的坐标;
(2)连接BM,易求扇形AMB的面积和△AMB的面积,由S弓形ACB=S扇形AMB﹣S△AMB计算即可;
(3)首先证△AMC为等边三角形,再根据等边三角形的三个内角都是60°和直径所对的圆周角∠ACP=90°可求得∠OCE=30°,然后在直角三角形OCE中利用30°角所对的直角边是斜边的一半来证明BE=2OE.
解:(1)连接PB,
∵PA是圆M的直径,
∴∠PBA=90°,
∴AO=OB=3,
又∵MO⊥AB,
∴PB∥MO,
∴PB=2OM=2![]()
∴P点坐标为(3,2![]() ),
),
在直角三角形ABP中,AB=6,PB=2![]() ,
,
根据勾股定理得:AP=![]() =4
=4![]() ,
,
∴圆的半径MC=2![]() ,
,
又∵OM=![]() ,
,
∴OC=MC﹣OM=![]() ,
,
则C(0,﹣![]() );
);
(2)连接BM,
∵BP=2![]() ,AP=4
,AP=4![]() ,
,
∴sin∠PAB=![]() ,
,
∴∠PAB=30°,
∴OM=![]() AM=
AM=![]() ,
,
∴S△AMB=![]() ABOM=
ABOM=![]() ×6×
×6×![]() =3
=3![]() ,
,
∵
∴∠AMB=120°,
∴S扇形AMB=![]() =4π,
=4π,
∴S弓形ACB=4π﹣![]() ;
;
(3)BE=20E,理由如下:
∵AM=MC=2![]() ,AO=3,OC=
,AO=3,OC=![]() ,
,
∴AM=MC=AC=2![]() ,
,
∴△AMC为等边三角形,
又∵AP为圆M的直径,
∴∠ACP=90°
∴∠OCE=30°,
∴OE=1,BE=2,
∴BE=2OE.


科目:初中数学 来源: 题型:
【题目】魔术师为大家表演魔术.他请观众想一个数,然后将这个数按以下步骤操作:

魔术师立刻说出观众想的那个数.
(1)如果小明想的数是﹣1,那么他告诉魔术师的结果应该是 ;
(2)如果小聪想了一个数并告诉魔术师结果为93,那么魔术师立刻说出小聪想的那个数是 ;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,请你说出其中的奥妙.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50度.
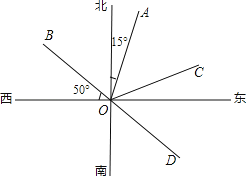
(1)若∠AOC=∠AOB,则OC的方向是 ;
(2)OD是OB的反向延长线,OD的方向是 ;
(3)∠BOD可看作是OB绕点O逆时针方向至OD,作∠BOD的平分线OE,OE的方向是 ;
(4)在(1)、(2)、(3)的条件下,∠COE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点.
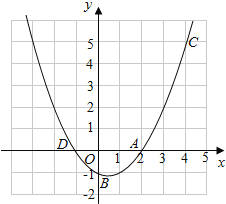
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
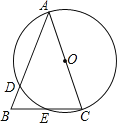
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.(在横线上填写正确的依据或证明步骤)
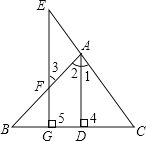
解答:是,理由如下:
∵AD⊥BC,EG⊥BC(已知)
∴∠4=∠5=90°(垂直的定义)
∴AD∥EG
∴∠1=∠E
∠2=∠3
∵∠E=∠3(已知)
∴∠ =∠ ;
∴AD是∠BAC的平分线(角平分线的定义).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)
(1) 填空:
(a-b)(a+b)=________;
(a-b)(a2+ab+b2)=________;
(a-b)(a3+a2b+ab2+b3)=________.
(2) 猜想:
(a-b)(an-1+an-2b+…+abn-2+bn-1)=________ (其中n为正整数,且n≥2).
(3) 利用(2)猜想的结论计算: 29-28+27-…+23-22+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com