
【题目】某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
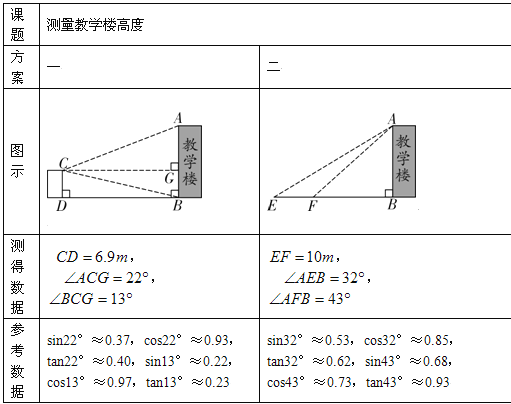
请你选择其中的一种方案,求教学楼的高度(结果保留整数).
【答案】教学楼的高度约19米.
【解析】
试题分析:若选择方法一,在Rt△BGC中,根据CG=![]() 即可得出CG的长,同理,在Rt△ACG中,根据tan∠ACG=
即可得出CG的长,同理,在Rt△ACG中,根据tan∠ACG=![]() 可得出AG的长,根据AB=AG+BG即可得出结论.
可得出AG的长,根据AB=AG+BG即可得出结论.
若选择方法二,在Rt△AFB中由tan∠AFB=![]() 可得出FB的长,同理,在Rt△ABE中,由tan∠AEB=
可得出FB的长,同理,在Rt△ABE中,由tan∠AEB=![]() 可求出EB的长,由EF=EB-FB且EF=10,可知
可求出EB的长,由EF=EB-FB且EF=10,可知![]() ,故可得出AB的长.
,故可得出AB的长.
试题解析:若选择方法一,解法如下:
在Rt△BGC中,∠BGC=90°,∠BCG=13°,BG=CD=6.9,
∵CG=![]() ,
,
在Rt△ACG中,∠AGC=90°,∠ACG=22°,
∵tan∠ACG=![]() ,
,
∴AG=30×tan22°≈30×0.40=12,
∴AB=AG+BG=12+6.9≈19(米).
答:教学楼的高度约19米.
若选择方法二,解法如下:
在Rt△AFB中,∠ABF=90°,∠AFB=43°,
∵tan∠AFB=![]() ,
,
∴FB=![]() ,
,
在Rt△ABE中,∠ABE=90°,∠AEB=32°,
∵tan∠AEB=![]() ,
,
∴EB=![]() ,
,
∵EF=EB-FB且EF=10,
∴![]() ,解得AB=18.6≈19(米).
,解得AB=18.6≈19(米).
答:教学楼的高度约19米.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:
【题目】如图1所示,已知抛物线y=-x2+4x+5的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.

(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,S△HGF:S△BGF=5:6?
(3)图2所示的抛物线是由y=-x2+4x+5向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前跑到400米以外的安全区域.已知导火线的燃烧速度是1.2厘米/秒,操作人员跑步的速度是5米/秒.为了保证操作人员的安全,导火线的长度要超过( )
A. 66厘米 B. 76厘米 C. 86厘米 D. 96厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设 y=|x﹣1|+|x+1|,则下面四个结论中正确的是( )
A. y 没有最小值 B. 只有一个 x 使 y 取最小值
C. 有限个 x(不止一个)y 取最小值 D. 有无穷多个 x 使 y 取最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;

(1)若点A、C的坐标分别为(-3,0)、(-2,3),请画出平面直角坐标系并指出点B的坐标;
(2)画出△ABC关于![]() 轴对称再向上平移1个单位后的图形△A1B1C1;
轴对称再向上平移1个单位后的图形△A1B1C1;
(3)以图中的点D为位似中心,将△A1B1C1作位似变换且把边长放大到原来的两倍,得到△A2B2C2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com