
����Ŀ����֪������y��x2+��1��2a��x��2a��a�dz�������
��1��֤��������������x�����н��㣻
��2�������������x���һ������ΪA��m��0������2��m��5����a��ȡֵ��Χ��
��3���ڣ�2���������£���aΪ����������������x���·��IJ�����x�����Ϸ��ۣ����ಿ�ֱ��ֲ��䣬�õ�һ����ͼ��G����������ͼ��̽��ֱ��y��kx+1��kΪ����������ͼ��G����������������
���𰸡���1������������2��1��a��![]() ����3����ͼ��G��������2����
����3����ͼ��G��������2����
��������
��1���������ߵ�yֵ����0��֤���÷��̵ġ���0���ɣ�
��2������A����������m��ֵ��������a��ȡֵ��Χ��
��3����k��0��k��0����������ۣ����ͼ�����⣮
�⣺��1����y��0����0��x2+��1��2a��x��2a��
�ߡ�����1��2a��2��4��1������2a������1+2a��2��0��
��x2+��1��2a��x��2a��0��ʵ������
�����������x�����н��㣻
��2������������x���һ������ΪA��m��0����
��0��m2+��1��2a��m��2a��
��m����1��m��2a��
��2��m��5��
��2��2a��5��
��1��a��![]() ��
��
��3����1��a��![]() ����a������
����a������
��a��2��
�������߽���ʽΪ��y��x2��3x��4��
��ͼ����k��0ʱ��
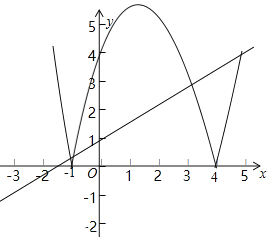
��y��kx+1���㣨��1��0��ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������3����
��k��1��
��0��k��1ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������4����
��k��1ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������2����
��ͼ����k��0ʱ��
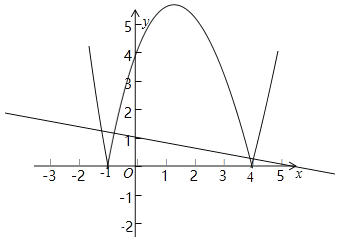
��y��kx+1���㣨4��0��ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������3����
��k����![]() ��
��
����![]() ��k��0ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������4����
��k��0ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������4����
��k����![]() ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������2����
ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������2����


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3�֣���ͬһƽ��ֱ������ϵ�У�����y=ax2+bx��y=bx+a��ͼ������ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
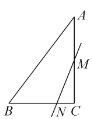
����Ŀ����֪����ͼ������ABC�У�AB=AC��DΪ��BC��һ�㣬��AB��BDΪ�ڱ���ƽ���ı���ABDE������AD��EC��
��1����֤����ADC�ա�ECD��
��2������D��ʲôλ��ʱ���ı���ADCE�Ǿ��Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
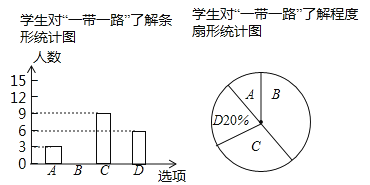
����Ŀ��ѧУ��֪�����꼶ѧ�����ҹ���������һ��һ·�����˽�̶ȣ������ȡ���־��꼶ѧ�������ʾ����飬�ʾ�����4��ѡ�ÿλ�������ѧ����ѡ��ֻѡһ���A���dz��˽⣮B���˽⣮C��֪��һ�㣮D����ȫ��֪����������Ľ����������������������ͳ��ͼ�����������ͳ��ͼ�е���Ϣ������������⣺
��1���ι������˶���ѧ����
��2����ȫ����ͳ��ͼ��
��3����У���꼶����600��ѧ��������������˽�����ѧ��Լ�ж�������
��4�������dz��˽�����3���У���2��Ů����1����������ʦ�����3������ѡ����������Ա�������б�����״ͼ�������ѡ�е�����ǡ����һ����һŮ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
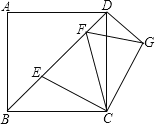
����Ŀ����ͼ����������ABCD�У�AB��a����E��F�ڶԽ���BD�ϣ��ҡ�ECF����ABD������BCE�Ƶ�C��תһ���ǶȺõ���DCG������FG�������н��ۣ�
�١�FCG����CDG��
�ڡ�CEF���������![]() ��
��
��FCƽ�֡�BFG��
��BE2+DF2��EF2��
������ȷ�Ľ�����_____������д������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ε�һ��ƽ����![]() �ᣬһ������
�ᣬһ������![]() ���ϣ����ڵ��⣬���ǵı߳�����Ϊ2��4��6��8����������������
���ϣ����ڵ��⣬���ǵı߳�����Ϊ2��4��6��8����������������![]() ��ʾ������
��ʾ������![]() ��
��![]() �ᡢ�ױ�
�ᡢ�ױ�![]() ��
��![]() ��
��![]() ���������һ����λ����
���������һ����λ����![]() ��������__________��
��������__________��![]() ��������__________��
��������__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ���ϵ��е㣬
���ϵ��е㣬![]() ��
��![]() ��������һ�㣬��
��������һ�㣬��![]() ������
������![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ǡ������
ǡ������![]() ����λ���ϣ���
����λ���ϣ���![]() __________��
__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�Ƶ�C˳ʱ����ת�õ���DEC��ʹ��A�Ķ�Ӧ��Dǡ�����ڱ�AB�ϣ���B�Ķ�Ӧ��ΪE������BE�������ĸ����ۣ���AC��AD����AB��EB����BC��EC���ܡ�A����EBC������һ����ȷ����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ�������У�������![]() ����
����![]() ����
����![]() ��ֱ��
��ֱ��![]() �Ϸ��������ϵ�һ���㣬
�Ϸ��������ϵ�һ���㣬![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ��
��
![]() ����������ϵ������������ͼ�����������ߵĺ�������ʽ��
����������ϵ������������ͼ�����������ߵĺ�������ʽ��
![]() ��
��![]() ʱ�����
ʱ�����![]() �����ꣻ
�����ꣻ
![]() ���߶�
���߶�![]() �����ֵ��
�����ֵ��
![]() ���߶�
���߶�![]() ���ʱ������
���ʱ������![]() ��ֱ��
��ֱ��![]() ����
����![]() ��ֱ��д����
��ֱ��д����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com