
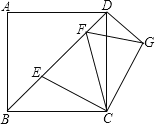
【题目】如图,在正方形ABCD中,AB=a,点E,F在对角线BD上,且∠ECF=∠ABD,将△BCE绕点C旋转一定角度后,得到△DCG,连接FG.则下列结论:
①∠FCG=∠CDG;
②△CEF的面积等于![]() ;
;
③FC平分∠BFG;
④BE2+DF2=EF2;
其中正确的结论是_____.(填写所有正确结论的序号)
【答案】①③④
【解析】
由正方形的性质可得AB=BC=CD=AD=a,∠ABD=∠CBD=∠ADB=∠BDC=45°,由旋转的性质可得∠CBE=∠CDG=45°,BE=DG,CE=CG,∠DCG=∠BCE,由SAS可证△ECF≌△GCF,可得EF=FG,∠EFC=∠GFC,S△ECF=S△CFG,即可求解.
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD=a,∠ABD=∠CBD=∠ADB=∠BDC=45°,
∴∠ECF=∠ABD=45°,
∴∠BCE+∠FCD=45°,
∵将△BCE绕点C旋转一定角度后,得到△DCG,
∴∠CBE=∠CDG=45°,BE=DG,CE=CG,∠DCG=∠BCE,
∴∠FCG=∠ECF=45°,
∴∠FCG=∠CDG=45°,故①正确,
∵EC=CG,∠FCG=∠ECF,FC=FC,
∴△ECF≌△GCF(SAS)
∴EF=FG,∠EFC=∠GFC,S△ECF=S△CFG,
∴CF平分∠BFG,故③正确,
∵∠BDG=∠BDC+∠CDG=90°,
∴DG2+DF2=FG2,
∴BE2+DF2=EF2,故④正确,
∵DF+DG>FG,
∴BE+DF>EF,
∴S△CEF<S△BEC+S△DFC,
∴△CEF的面积<![]() S△BCD=
S△BCD=![]() ,故②错误;
,故②错误;
故答案为:①③④


科目:初中数学 来源: 题型:
【题目】京剧脸谱是京剧艺术独特的表现形式京剧表演中,经常用脸谱象征人物的性格,品质,甚至角色和命运如红脸代表忠心耿直,黑脸代表强悍勇猛现有三张不透明的卡片,其中两张卡片的正面图案为“红脸”,另外张卡片的正面图案为“黑脸”,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.

(1)请用画树状图或列表的方法,求抽出的两张卡片上的图案都是“红脸”的概率(图案为“红脸”的两张卡片分别记为![]() 、
、![]() ,图案为“黑脸”的卡片记为
,图案为“黑脸”的卡片记为![]() );
);
(2)若第一次抽出后不放回,请直接写出求抽出的两张卡片上的图案都是“红脸”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
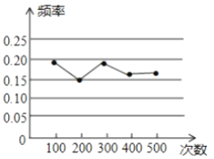
【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从厂家选购甲、乙两种商品,乙商品每件进价比甲商品每件进价少20元,若购进甲商品5件和乙商品4件共需要1000元;
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)若甲种商品的售价为每件145元,乙种商品的售价为每件120元,该商店准备购进甲、乙两种商品共40件,且这两种商品全部售出后总利润不少于870元,则甲种商品至少可购进多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
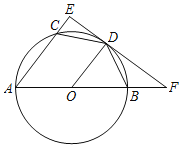
【题目】如图,已知AB为⊙O的直径,点C、D在⊙O上,CD=BD,E、F是线段AC、AB的延长线上的点,并且EF与⊙O相切于点D.
(1)求证:∠A=2∠BDF;
(2)若AC=3,AB=5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(1﹣2a)x﹣2a(a是常数).
(1)证明:该抛物线与x轴总有交点;
(2)设该抛物线与x轴的一个交点为A(m,0),若2<m≤5,求a的取值范围;
(3)在(2)的条件下,若a为整数,将抛物线在x轴下方的部分沿x轴向上翻折,其余部分保持不变,得到一个新图象G,请你结合新图象,探究直线y=kx+1(k为常数)与新图象G公共点个数的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框
上,通过推动左侧活页门开关;图2是其俯视图简化示意图,已知轨道![]() ,两扇活页门的宽
,两扇活页门的宽![]() ,点
,点![]() 固定,当点
固定,当点![]() 在
在![]() 上左右运动时,
上左右运动时,![]() 与
与![]() 的长度不变(所有结果保留小数点后一位).
的长度不变(所有结果保留小数点后一位).
(1)若![]() ,求
,求![]() 的长;
的长;
(2)当点![]() 从点
从点![]() 向右运动60
向右运动60![]() 时,求点
时,求点![]() 在此过程中运动的路径长.
在此过程中运动的路径长.
(参考数据:sin50°≈0.77, cos50°≈0.64, tan50°≈1.19, π取3.14)

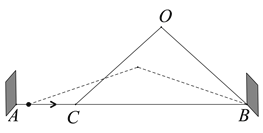
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
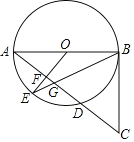
【题目】如图,在⊙O中,AB是⊙O的直径,F是弦AD的中点,连结OF并延长OF交⊙O于点E,连结BE交AD于点G,延长AD至点C,使得GC=BC,连结BC.
(1)求证:BC是⊙O的切线.
(2)⊙O的半径为10,sinA=![]() ,求EG的长.
,求EG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的动点(不与端点重合),且
上的动点(不与端点重合),且![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .给出如下几个结论:
.给出如下几个结论:
①![]()
②![]() 平分
平分![]() ;
;
③若![]() ,则
,则![]()
④![]()
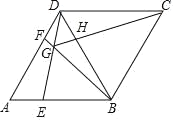
其中正确的结论是_____________(填写所有正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com