Question

【题目】如图，在等腰Rt△ABC中，∠C＝90°，D是斜边上AB上任一点，AE⊥CD于E ， BF⊥CD交CD的延长线于F ， CH⊥AB于H点，交AE于G ．

（1）试说明AH＝BH
（2）求证：BD＝CG ．
（3）探索AE与EF、BF之间的数量关系

Answer 1

【答案】
（1）解：∵AC=BC，CH⊥AB∴AH＝BH
（2）解：∵ABC为等腰直角三角形，且CH⊥AB

∴∠ACG＝45°

∵∠CAG＋∠ACE＝90°，∠BCF＋∠ACE＝90°

∴∠CAG＝∠BCF

在△ACG和△CBD中

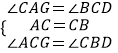
∴△ACG≌△CBD（ASA）

∴BD＝CG

（3）解：AE=EF＋BF

理由如下：

在△ACE和△CBF中，

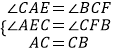
∴△ACE≌△CBF， ∴AE=CF，CE=BF， ∴AE=CF=CE+EF=BF+EF

【解析】第1小题，根据等腰三角形三线合一可求解；第2小题，根据等腰直角三角形的性质和直角三角形两锐角互余可找出条件证明△ACG≌△CBD；第3小题，由前面的条件可证△ACE≌△CBF，得到AE=CF，CE=BF，从而得到AE=CF=CE+EF=BF+EF。