
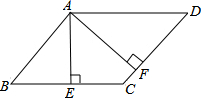
 如图,?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=135°.
如图,?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=135°.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
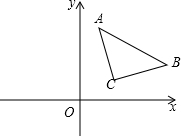 平面直角坐标系上点A(1,4),点B(5,2),点C(2,1),若x轴上有一点D,使点A和点B到直线CD的距离相等,那么满足条件的点D的坐标是(4,0).
平面直角坐标系上点A(1,4),点B(5,2),点C(2,1),若x轴上有一点D,使点A和点B到直线CD的距离相等,那么满足条件的点D的坐标是(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
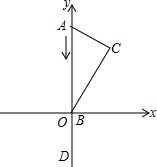 如图,将含30°的直角三角尺放在如图所示的直角坐标系中,点A(0,4),点B在原点,∠C=90°,∠ABC=30°,D点与A点关于原点对称,A点向D点运动,到达D点后停止.B点在x轴上运动.当A到达D时,点C走过的路径长为4$\sqrt{3}$.
如图,将含30°的直角三角尺放在如图所示的直角坐标系中,点A(0,4),点B在原点,∠C=90°,∠ABC=30°,D点与A点关于原点对称,A点向D点运动,到达D点后停止.B点在x轴上运动.当A到达D时,点C走过的路径长为4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
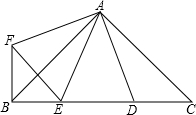 如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )| A. | △AED≌△AEF | B. | △ABE∽△ACD | C. | BE+DC>DE | D. | BE2+DC2=DE2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
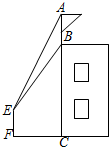 如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m,
如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com