
分析 先根据一元二次方程的解的定义得到m2-3m-1=0,即m2=3m+1,再把m3-2m2+4n化简用m和n的一次式表示得到m3-2m2+4n=4(m+n)+1,而根据根与系数的关系得到m+n=3,然后利用整体代入的方法计算即可.
解答 解:∵m是方程x2-3x-1=0的根,
∴m2-3m-1=0,
∴m2=3m+1,
∴m3-2m2+4n=m(m2-2m)+4n=m(3m+1-2m)+4n=m2+m+4n=3m+1+m+4n=4(m+n)+1,
∵m,n是方程x2-3x-1=0的两根,
∴m+n=3,
∴m3-2m2+4n=4×3+1=13.
故答案为13.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了一元二次方程的解.


科目:初中数学 来源: 题型:解答题
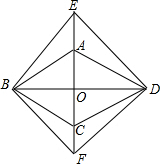 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
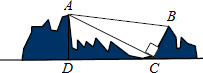 如图,某景区有一出索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,求山峰顶点A到C点的水平面高度AD.(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)
如图,某景区有一出索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,求山峰顶点A到C点的水平面高度AD.(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
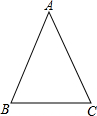 如图,△ABC中,AB=AC=20,cosC=$\frac{\sqrt{5}}{5}$.
如图,△ABC中,AB=AC=20,cosC=$\frac{\sqrt{5}}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com