
【题目】将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1 , B1C1交CD于点E,AB= ![]() ,则四边形AB1ED的内切圆半径为( )
,则四边形AB1ED的内切圆半径为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:作∠DAF与∠AB1G的角平分线交于点O,过O作OF⊥AB1 ,
则∠OAF=30°,∠AB1O=45°,
故B1F=OF= ![]() OA,
OA,
设B1F=x,则AF= ![]() ﹣x,
﹣x,
故( ![]() ﹣x)2+x2=(2x)2 ,
﹣x)2+x2=(2x)2 ,
解得x= ![]() 或x=
或x= ![]() (舍去),
(舍去),
∴四边形AB1ED的内切圆半径为: ![]() .
.
故选:B.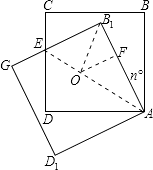
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对三角形的内切圆与内心的理解,了解三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.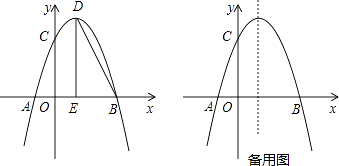
(Ⅰ)求抛物线的解析式及点D的坐标;
(Ⅱ)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(Ⅲ)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc﹣ad.
例如:(1,2)★(3,4)=2×3﹣1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,﹣3)★(3,﹣2)= ;
(2)若有理数对(﹣3,2x﹣1)★(1,x+1)=7,则x= ;
(3)当满足等式(﹣3,2x﹣1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.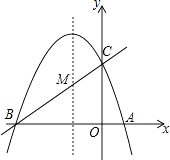
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件画图
如图示点A、B、C分别代表三个村庄.
(1)画射线AC;
(2)画线段AB;
(3)若线段AB是连结A村和B村的一条公路,现C村庄也要修一条公路与A、B两村庄之间的公路连通,为了减少修路开支,C村庄应该如何修路?请在同一图上用三角板画出示意图,并说明画图理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N.求证:△ABN≌△CDM.

查看答案和解析>>
科目:初中数学 来源: 题型:
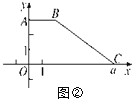
【题目】如图①,在平面直角坐标系xOy中,已知点A(0,3),B(2,3),OC=a.将梯形ABCO沿直线y=x折叠,点A落在线段OC上,对应点为E.
(1)求点E的坐标;
(2)①若BC∥AE,求a的值;(提示:两边互相平行的四边形是平行四边形,平行四边形的对边相等)
②如图②,若梯形ABCO的面积为2a,且直线y=mx将此梯形面积分为1∶2的两部分,求直线y=mx的函数表达式.
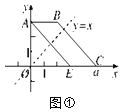
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健向器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com