
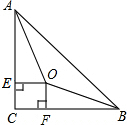
 如图所示,△ABC中,∠C=90°,∠CAB、∠CBA的角平分线交于O点,OE⊥AC于E,OF⊥BC于F.
如图所示,△ABC中,∠C=90°,∠CAB、∠CBA的角平分线交于O点,OE⊥AC于E,OF⊥BC于F.分析 (1)过O作OG⊥AB于G,由角平分线的性质可求出OF=OE,由正方形的判定定理即可证明;
(2)先利用HL证明Rt△AOE≌Rt△AOG,得出AE=AG,同理BF=BG,那么AC+BC-AB=(AE+EC)+(BF+FC)-(AG+BG)=EC+FC,再由四边形CEOF为正方形,得到EC=FC=OF=$\frac{3}{2}$,于是AC+BC-AB=3.
解答 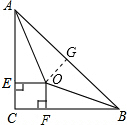 (1)证明:过O作OG⊥AB于G,
(1)证明:过O作OG⊥AB于G,
∵∠CAB、∠CBA的角平分线交于O点,OE⊥AC于E,OF⊥BC于F,
∴OF=OG,OE=OG,
∴OF=OE,
∵△ABC是直角三角形,∠C=90°,DE⊥BC于E,DF⊥AC于F,
∴四边形CEOF为正方形;
(2)解:在Rt△AOE与Rt△AOG中,
$\left\{\begin{array}{l}{OA=OA}\\{OE=OG}\end{array}\right.$,
∴Rt△AOE≌Rt△AOG(HL),
∴AE=AG,
同理BF=BG,
∴AC+BC-AB=(AE+EC)+(BF+FC)-(AG+BG)=EC+FC,
∵四边形CEOF为正方形,
∴EC=FC=OF=$\frac{3}{2}$,
∴AC+BC-AB=3.
点评 本题考查了正方形的判定与性质,角平分线的性质,全等三角形的判定与性质.准确作出辅助线,得出OF=OE是解决第(1)问的关键;证明出AE=AG,BF=BG是解决第(2)问的关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:选择题
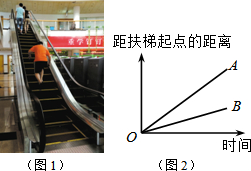 大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )
大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )| A. | 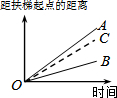 | B. | 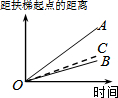 | C. | 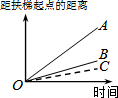 | D. | 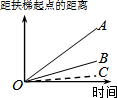 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 组别 | 第一组 | 第二组 | 第三组 | 第四组 |
| 年龄段(岁) | 27<x≤31 | 31<x≤34 | 34<x≤37 | 37<x≤40 |
| 频数(人) | 8 | 11 | 17 | 20 |
| A. | 第一组 | B. | 第二组 | C. | 第三组 | D. | 第四组 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com