
【题目】如图所示,△ABC中,D为AB的中点,DC⊥AC,且∠BCD=30°,求∠CDA的正弦值、余弦值、正切值和余切值.
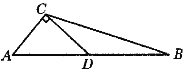
【答案】![]() ;
;![]() ;
;![]() ;
;![]()
【解析】
过D作DE∥AC,交BC于点E,由平行线等分线段定理,根据D为AB中点,得到E为CB中点,可得出DE为三角形ABC中位线,利用中位线定理得到AC=2DE,由两直线平行内错角相等及垂直定义得到DE垂直与CD,在直角三角形CDE中,利用30度所对的直角边等于斜边的一半得到CE=2DE,利用勾股定理表示出DC与AD,利用锐角三角函数定义即可求出∠CDA的正弦值、余弦值和正切值.
过D作DE∥AC,交BC于点E.
∵ AD=BD,∴ CE=EB,∴ AC=2DE.
又∵ DC⊥ AC,DE∥AC,
∴ DC⊥DE,即∠CDE=90°.
又∵ ∠BCD=30°,∴ EC=2DE,DC=![]() DE.
DE.
设DE=k,则CD=![]() ,AC=2k.
,AC=2k.
在Rt△ACD中,![]() .
.
∴ ![]() ,
,![]() .
.
![]() .
.![]() .
.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
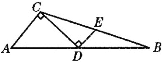
【题目】如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=![]() NF;③
NF;③![]() ;④S四边形CGNF=
;④S四边形CGNF=![]() S四边形ANGD.其中正确的结论的序号是 .
S四边形ANGD.其中正确的结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
(1)求抛物线的表达式;
(2)如图,当CP//AO时,求∠PAC的正切值;
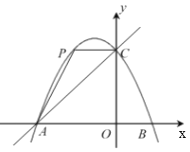
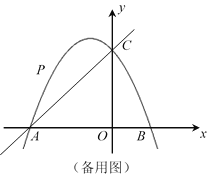
(3)当以AP、AO为邻边的平行四边形第四个顶点恰好也在抛物线上时,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的周长是48cm, AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C.

(1)求∠C的度数;
(2)已知DF的长是关于x的方程x2-5x-a=0的一个根,求该方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=-![]() x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.

(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
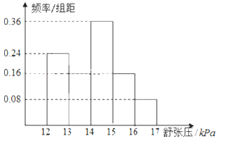
【题目】为了研究某药品的疗效,现选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组、第二组、…、第五组.如图是根据试验数据制成的频率分布直方图.
(1)若第一组接受治疗的志愿者有12人,则第三组接受治疗的志愿者有多少人?
(2)若接受治疗的志愿者共有50人,规定舒张压在14kpa以上的志愿者接受进一步的临床试验,若从三组志愿者中按比例分配20张床位,则舒张压数据在[14,15)的志愿者总共可以得到多少张床位?
查看答案和解析>>
科目:初中数学 来源: 题型:
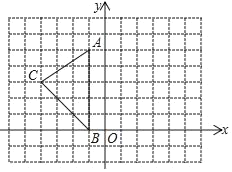
【题目】如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3)
(1)将△ABC向右平移6个单位至△A1B1C1,再将△A1B1C1绕点E(5,1)逆时针旋转90°至△A2B2C2,请按要求画出图形;
(2)在(1)的变换过程中,直接写出点C的运动路径长
(3)△A2B2C2可看成△ABC绕某点P旋转90°得到的,则点P的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com