
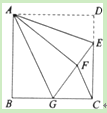
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
![]()
【答案】C
【解析】①正确.因为AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴△ABG≌△AFG;
②正确.因为:EF=DE=![]() CD=2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.所以BG=3=6﹣3=GC;
CD=2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.所以BG=3=6﹣3=GC;
③正确.因为CG=BG=GF,所以△FGC是等腰三角形,∠GFC=∠GCF.又∠AGB=∠AGF,∠AGB+∠AGF=180°﹣∠FGC=∠GFC+∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF;
④错误.
过F作FH⊥DC,
∵BC⊥DH,
∴FH∥GC,
∴△EFH∽△EGC,
∴![]() =
=![]() ,
,
EF=DE=2,GF=3,
∴EG=5,
∴![]() =
=![]() =
=![]() ,
,
∴S△FGC=S△GCE﹣S△FEC=![]() ×3×4﹣
×3×4﹣![]() ×4×(
×4×(![]() ×3)=
×3)=![]() ≠3.
≠3.
故选C.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】杭州某游乐园门票价格为每人100元,20人以上(含20人)的团体票8折优惠.
(1)建兰中学初二年级一等奖学金获得者共有18人,学校奖励他们去游玩,你认为学校买18张门票,还是多买2张(买20张)购团体票更合算?
(2)如果获奖的学生不足20人,那么人数达到多少人时购买团体票比买普通票更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如(图1),点![]() 把线段
把线段![]() 分割成
分割成![]() 和
和![]() ,若以
,若以![]() 为边的三角形是一个直角三角形,则称点
为边的三角形是一个直角三角形,则称点![]() 是线段
是线段![]() 的勾股分割点.
的勾股分割点.
(1)已知点![]() 是线段
是线段![]() 的勾股分割点,若
的勾股分割点,若![]() ,求
,求![]() 的长;
的长;
(2)如(图2),在等腰直角![]() 中,
中, ![]() ,点
,点![]() 为边
为边![]() 上两点,满足
上两点,满足![]() ,求证:点
,求证:点![]() 是线段
是线段![]() 的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把
的勾股分割点;阳阳同学在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 试一试.请根据陈老师的提示完成第(2)小题的证明过程.
试一试.请根据陈老师的提示完成第(2)小题的证明过程.
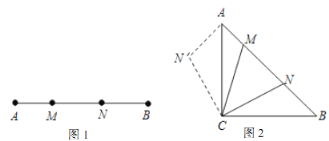
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=17,BC=21,AC=10,动点P从点C出发,沿着CB运动,速度为每秒3个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:
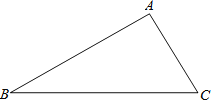
(1)求BC上的高;
(2)当t为何值时,△ACP为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
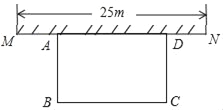
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料.
(1)设计一种砌法,使矩形花园的面积为300m2.
(2)当BC为何值时,矩形ABCD的面积有最大值?并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )

A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
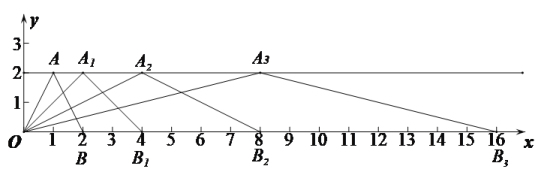
【题目】如下图所示,在直角坐标系中,第一次将△OAB变换成![]() ,第二次将
,第二次将![]() 变换成
变换成![]() ,第三次将
,第三次将![]() 变换成
变换成![]() ,已知
,已知![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将![]() 变换成
变换成![]() ,则
,则![]() 的坐标为 ,
的坐标为 ,![]() 的坐标为 .
的坐标为 .
(2)可以发现变换过程中![]() ……
……![]() 的纵坐标均为 .
的纵坐标均为 .
(3)按照上述规律将△OAB进行n次变换得到![]() ,则可知
,则可知![]() 的坐标为 ,
的坐标为 , ![]() 的坐标为 .
的坐标为 .
(4)线段![]() 的长度为 .
的长度为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com