
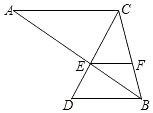
【题目】如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.
(1)求EF的长;
(2)如果△BEF的面积为4,求△ABC的面积.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】数据共50个,分别落在5个小组内,第一、二、三、四组的数据分别为2、8、15、14,则第五个小组的频数为( )
A.14
B.15
C.10
D.11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量调查对象每分钟的心跳次数,甲同学建议测量2分钟的心跳次数再除以2,乙同学建议测量10秒的心跳次数再乘以6,你认为哪位同学的方法更具有代表性( )
A.甲同学
B.乙同学
C.两种方法都具有代表性
D.两种方法都不合理
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图形的操作过程:
在图①中,将线段A1A2向右平移1个单位到B1B2 , 得到封闭图形A1A2B2B1(即阴影部分);
在图②中,将折线A1A2A3向右平移1个单位到B1B2B3 , 得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影; 
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:
S1= , S2= , S3= .
(3)联想与探索:
如图④在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少并说明你的猜想是正确的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB∥CD,猜想∠BPD与∠B,∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,不需要说明理由. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com