
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 于点
于点![]() 交
交![]() 于
于![]() 点,延长
点,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() .
.

(1)证明:四边形![]() 是矩形;
是矩形;
(2)当![]() 时,猜想线段
时,猜想线段![]() 、
、![]() 、
、![]() 的数量关系,并证明.
的数量关系,并证明.
【答案】(1)详见解析;(2)![]() ,证明详见解析
,证明详见解析
【解析】
(1)根据平行四边形的性质得到AD∥BC,AD=BC,进而求出AD=FH,再根据平行四边形的判定得出四边形AFHD是平形四边形,最后根据矩形的判定得出即可得到答案;
(2)根据平行四边形的性质得到AB∥CD,求出∠1=∠3,推出AE=AD,再根据正方形的判定和性质得出AD=DH,求出△DAG≌△DHM,最后根据全等三角形的性质得出∠2=∠3=∠HDM,∠AGD=∠M,求出∠M=∠CDM即可得到答案.
(1)∵四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]() (平行四边形对边平行且相等),
(平行四边形对边平行且相等),
∵![]()
∴![]() ,
,
∴![]() (等量替换),
(等量替换),
∴四边形![]() 是平行四边形(对边平行且相等的四边形是平行四边形),
是平行四边形(对边平行且相等的四边形是平行四边形),
∵![]() ∴
∴![]() ,
,
∴平行四边形![]() 是矩形;
是矩形;
(2)猜想:![]()
证明:如图,延长![]() 至
至![]() 使
使![]() ,连接
,连接![]() ,
,

∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ∴
∴![]() ,
,
∵![]() 平分
平分![]() ∴
∴![]() ∴
∴![]() ∴
∴![]() ,
,
∵![]() ∴
∴![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
在△DAG和△DHM中,

∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ;
;


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】阅读理(解析)
提出问题:如图1,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
当AP=![]() AD时(如图2):
AD时(如图2):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD,
S△ABD,
∵PD=AD﹣AP=![]() AD,△CDP和△CDA的高相等
AD,△CDP和△CDA的高相等
∴S△CDP=![]() S△CDA,
S△CDA,
∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP=S四边形ABCD﹣![]() S△ABD﹣
S△ABD﹣![]() S△CDA,
S△CDA,
=S四边形ABCD﹣![]() (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣![]() (S四边形ABCD﹣S△ABC)=
(S四边形ABCD﹣S△ABC)=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
(1)当AP=![]() AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
(2)当AP=![]() AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
(3)一般地,当AP=![]() AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
(4)当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .

查看答案和解析>>
科目:初中数学 来源: 题型:
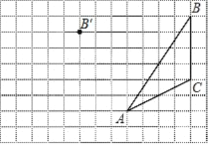
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD
(3)画出BC边上的高线AE
(4)点![]() 为方格纸上的格点(异于点
为方格纸上的格点(异于点![]() ),若
),若![]() ,则图中的格点
,则图中的格点![]() 共有 个.
共有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
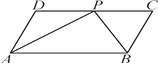
(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, ![]() ,
, ![]() ∥
∥![]() 轴,
轴, ![]() .
.

⑴.求点![]() 的坐标:
的坐标:
⑵.四边形![]() 的面积
的面积![]() 四边形
四边形![]() ;
;
⑶. 在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() △
△![]() =
= ![]() 四边形
四边形![]() ;若存在,求出点
;若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,![]() D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且![]() 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使![]() ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF

(1)求证:四边形EDFG是正方形;
(2)直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com