【题目】如图，在正方形ABCD的外侧，作等边三角形ADE，连接BE，CE．
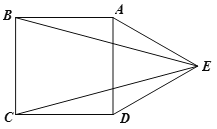
（1）求证：BE=CE．
（2）求∠BEC的度数
【答案】（1）证明见解析；（2）30°
【解析】
试题分析：（1）由正方形和等边三角形的性质得出AB=AE，DC=DE，∠BAE=150°，∠CDE=150°，可证ΔBAE≌ΔCDE，即可证出BE=CE；
（2）由（1）知：∠AEB=∠CED=15°，从而可求∠BEC的度数．
试题解析：（1）证明：∵四边形ABCD为正方形
∴AB=AD=CD,∠BAD=∠ ADC=90°
∵三角形ADE为正三角形
∴ AE=AD=DE,∠EAD=∠EDA=60°
∴∠BAE=∠CDE=150°
∴ΔBAE≌ΔCDE
∴BE=CE
（2）∵AB=AD, AD=AE,
∴AB=AE
∴∠ABE=∠AEB
又 ∵∠BAE=150° ∴∠ABE=∠AEB=15°
同理：∠CED=15°
∴∠BEC=600－15°×2=30°
金钥匙试卷系列答案科目：初中数学 来源： 题型：
【题目】为了丰富同学们的课余生活，某学校举行“亲近大自然”户外活动，现随机抽取了部分学生进行主题为“你最想去的景点是？”的问卷调查，要求学生只能从“A（植物园），B（花卉园），C（湿地公园），D（森林公园）”四个景点中选择一项，根据调查结果，绘制了如下两幅不完整的统计图．
请解答下列问题：
（1）本次调查的样本容量是 ；
（2）补全条形统计图；
（3）若该学校共有3600名学生，试估计该校最想去湿地公园的学生人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合)，PE⊥BC于点E，PF⊥CD于点F，连接EF给出下列五个结论：①AP＝EF；②AP⊥EF；③仅有当∠DAP＝45°或67.5°时，△APD是等腰三角形；④∠PFE＝∠BAP：⑤
PD＝EC．其中有正确有( )个．
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形
的对角线交于点
点
，
分别在
，
上（
）且
，
，
的延长线交于点
，
，的延长线交于点
，连接
.
（1）求证：
.
（2）若正方形的边长为4，为
的中点，求的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2019年4月23日是第24个世界读书日．为了弘扬中华传统文化，我县某学校举办了“让读书成为习惯，让书香飘满校园”主题活动，为此特为每个班级订购了一批新的图书．初一(1)班订购老舍文集4套和四大名著2套，总费用为480元；初一(2)班订购老舍文集2套和四大名著3套，总费用为520元．
(1)求老舍文集和四大名著每套各是多少元？
(2)学校准备再购买老舍文集和四大名著共20套，总费用不超过1720元，购买老舍文集的数量不超过四大名著的3倍，问学校有几种购买方案，请你设计出来．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
