
 如图所示,AB∥CD,O为∠A、∠C的平分线的交点,OE⊥AC于E,且OE=4,则AB与CD之间的距离等于8.
如图所示,AB∥CD,O为∠A、∠C的平分线的交点,OE⊥AC于E,且OE=4,则AB与CD之间的距离等于8. 分析 过点O作OF⊥AB于F,作OG⊥CD于G,然后根据角平分线上的点到角的两边的距离相等可得OE=OF=OG,再根据两直线平行,同旁内角互补求出∠BAC+∠ACD=180°,然后求出∠EOF+∠EOG=180°,从而判断出E、O、G三点共线,然后求解即可.
解答 解:过点O作OF⊥AB于F,作OG⊥CD于G,
∵O为∠BAC、∠DCA的平分线的交点,OE⊥AC,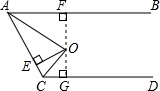
∴OE=OF,OE=OG,
∴OE=OF=OG=4,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠EOF+∠EOG=(180°-∠BAC)+(180°-∠ACD)=180°,
∴E、O、G三点共线,
∴AB与CD之间的距离=OF+OG=4+4=8.
故答案为:8.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,平行线的性质,熟记性质是解题的关键,难点在于作出辅助线并证明E、O、G三点共线.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李强家里搞装修时,木工师傅想要在一块矩形木板ABCD的中央挖去一个形状与原矩形相同,周长是原矩形一半的小矩形(如图),木工师傅算来算去,不知如何下手,正犯愁时,李强放学回家,见状说:“很方便,连接AC,BD交于点O,用刻度尺分别量出AO,BO,CO,DO的中点E,F,G,H,依次连接EF,FG,GH,HE,就得到要挖去的矩形EFGH.”请你说明道理.
李强家里搞装修时,木工师傅想要在一块矩形木板ABCD的中央挖去一个形状与原矩形相同,周长是原矩形一半的小矩形(如图),木工师傅算来算去,不知如何下手,正犯愁时,李强放学回家,见状说:“很方便,连接AC,BD交于点O,用刻度尺分别量出AO,BO,CO,DO的中点E,F,G,H,依次连接EF,FG,GH,HE,就得到要挖去的矩形EFGH.”请你说明道理.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 数字0也是单项式 | B. | -$\frac{2ab}{3}$的系数是-$\frac{2}{3}$ | ||
| C. | 1-a-ab是二次三项式 | D. | 多项式2x2+3x-5中,常数项为5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
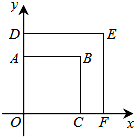 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:$\sqrt{2}$,点B的坐标为(1,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$).
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:$\sqrt{2}$,点B的坐标为(1,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,A、B、C三点的坐标分别为A(-6,7)、B(-3,0)、C(0,3).
在平面直角坐标系中,A、B、C三点的坐标分别为A(-6,7)、B(-3,0)、C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
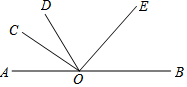 如图,已知点O在直线AB上,∠COE=90°,OD平分∠AOE,∠COD=25°,则∠BOD的度数为( )
如图,已知点O在直线AB上,∠COE=90°,OD平分∠AOE,∠COD=25°,则∠BOD的度数为( )| A. | 100° | B. | 115° | C. | 65° | D. | 130° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com