
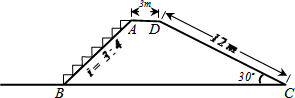
分析 作AE⊥BC于E,DF⊥BC于F.先解直角△DCF,求出DF=$\frac{1}{2}$DC=6m,则AE=DF=6m.再解直角△ABE,由$\frac{AE}{BE}$=$\frac{3}{4}$,求出BE=8m,那么地毯的长度为:AE+BE+AD+DC,代入数据计算,进而求得地毯的总花费.
解答 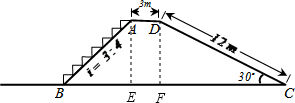 解:如图,作AE⊥BC于E,DF⊥BC于F.
解:如图,作AE⊥BC于E,DF⊥BC于F.
在直角△DCF中,∵∠DFC=90°,∠C=30°,DC=12m,
∴DF=$\frac{1}{2}$DC=6m,
∴AE=DF=6m.
在直角△ABE中,∵∠AEB=90°,i=3:4,
∴$\frac{AE}{BE}$=$\frac{3}{4}$,
∴BE=8m,
∴地毯的长度为:6+8+3+12=29(m),
∵地毯的面积为29×2=58(平方米),
∴地毯的总花费是120×58=6960(元).
答:总共要29m的地毯,若每平方米的地毯为120元,问所需地毯的总花费是6960元.
点评 本题考查了解直角三角形的应用-坡度坡角问题,准确作出辅助线构造直角三角形是解题的关键,理解在左面斜坡上所铺地毯的长度为AE+BE是本题的难点.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
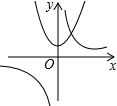 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}-{x}^{2}$-1>0的解集是( )| A. | x>1 | B. | x<-1 | C. | 0<x<1 | D. | -1<x<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com