
����Ŀ����֪����ͼ�٣���ABC����AED������ȫ�ȵĵ���ֱ�������Σ��䶥��B��E�غϣ�����BAC=��AED=90�㣬OΪBC���е㣬FΪAD���е㣬����OF��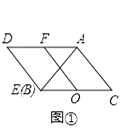
��1�����ⷢ��
����ͼ�٣��߶�OF��EC��������ϵΪ��
�ڽ���AED�Ƶ�A��ʱ����ת45�㣬��ͼ�ڣ�OF��EC��������ϵΪ��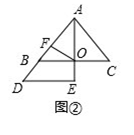
��2���������
��ͼ���С�AED�Ƶ�A��ʱ����ת����ͼ����ʾ��λ�ã����ж��߶�OF��EC��������ϵ��������֤����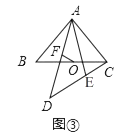
��3����չ̽��
��ͼ���С�AED�Ƶ�A��ʱ����ת����ת��Ϊ����0��ܦ���90�㣬AD= ![]() ����AED����ת�����У����ڡ�ACDΪֱ�������Σ���ֱ��д���߶�CD�ij���
����AED����ת�����У����ڡ�ACDΪֱ�������Σ���ֱ��д���߶�CD�ij���
���𰸡�
��1��OF= ![]() EC��OF=
EC��OF= ![]() EC
EC
��2��
�⣺OF= ![]() EC��
EC��
֤�����ڵ���ֱ�ǡ�ADE�У�FΪAD���е㣬
��AF= ![]() AD=
AD= ![]() AE��
AE��
�ڵ���ֱ�ǡ�ABC�У�OΪBC���е㣬
��ͼ1��
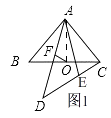
����AO��
��AO= ![]() AC����BAO=��CAO=45�㣬
AC����BAO=��CAO=45�㣬
�ߡ�DAE=45�㣬
���DAE=��CAO��
���DAE����EAO=��CAO����EAO��
����DAO=��CAE��
��AE=AC��
��AF=AO��
�� ![]() =
= ![]() ��
��
���AFO�ס�AEC��
�� ![]() =
= ![]() =
= ![]() ��
��
��OF= ![]() EC��
EC��
��3��
�⣺�ߡ�ABC�͡�AED������ȫ�ȵĵ���ֱ�������Σ�
��AD=BC= ![]() ��
��
��ED=AE=AB=AC=1��
��ACDΪֱ��������ʱ�������������
�ٵ�AD��AB�غ�ʱ����ͼ2��
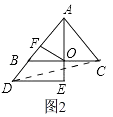
����CD��
�ߡ�ACDΪֱ�������Σ�AD��AC��
������ADE��ʱ����ת45�㣬
��AD= ![]() ��AC=1��
��AC=1��
���ɹ��ɶ����ɵ�CD= ![]() =
= ![]() ��
��
�ڵ�AE��AC�غ�ʱ����ͼ3��
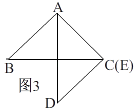
��ACDΪֱ�������Σ�AC��CD��
������ADE��ʱ����ת90�㣬��ʱCD=AC=1��
����CD�ij�Ϊ ![]() ��1��
��1��
���������⣺��1���١ߡ�ABC����AED������ȫ�ȵĵ���ֱ�������Σ�
��AD=BC��
��OΪBC���е㣬FΪAD���е㣬
��AF=OC��
�ߡ�BAC=��AED=90�㣬
��AD��BC��
���ı���AFOC��ƽ���ı��Σ�
��OF=AC= ![]() EC��
EC��
�ʴ𰸣�OF= ![]() EC������ͼ��
EC������ͼ��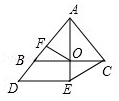
��AO= ![]() AC����BAO=��CAO=45�㣬
AC����BAO=��CAO=45�㣬
�ߡ�DAE=45�㣬
���DAE=��CAO��
���DAE����EAO=��CAO����EAO��
����DAO=��CAE��
��AE=AC��
��AF=AO��
�� ![]() =
= ![]() ��
��
���AFO�ס�AEC��
�� ![]() =
= ![]() =
= ![]() ��
��
��OF= ![]() EC��
EC��
�ʴ�OF= ![]() EC
EC
�����㾫����������Ĺؼ������������������ε�Ӧ�õ����֪ʶ�����ղ�ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�BC�Ĵ�ֱƽ����EF����ABC��ƽ����BD��E�������BAC=60�㣬��ACE=24�㣬��ô��BCE�Ĵ�С�ǣ�������

A. 24�� B. 30�� C. 32�� D. 36��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y=ax2��5ax+4a��x�ύ��A��B��A����B�����ࣩ��y�ύ�ڵ�C��
��1����ͼ1������AC��BC������ABC�����Ϊ3ʱ���������ߵĽ���ʽ��
��2����ͼ2����PΪ����������������һ�㣬����PC������BCP=2��ABCʱ�����P�ĺ����ꣻ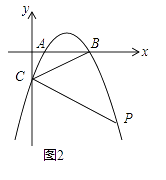
��3����ͼ3���ڣ�2���������£���F��AP�ϣ�����P��PH��x����H�㣬��K��PH���ӳ����ϣ�AK=KF����KAH=��FKH��PF=��4 ![]() a������KB���ӳ����������ڵ�Q����PQ�ij���
a������KB���ӳ����������ڵ�Q����PQ�ij���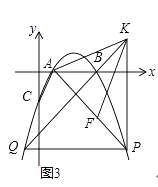
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������20��������1200̨GH�͵��Ӳ�Ʒ����������֪ÿ̨GH�Ͳ�Ʒ��4��G��װ�ú�3��H��װ��������ɣ���������80�����ˣ�ÿ������ÿ���ܼӹ�6��G��װ�û�3��H��װ�ã����������й��˷ֳ�����ͬʱ��ʼ�ӹ���ÿ��ֱ�ӹ�һ��װ�ã���Ҫ��ÿ��ӹ���G��H��װ����������ȫ���������GH�Ͳ�Ʒ��
��1������������������ʽ������ÿ����������ɶ�����GH�͵��Ӳ�Ʒ�����г���Ԫһ�η�����������⣮
��2��Ϊ���ڹ涨�������������������������һЩ�¹��ˣ���Щ�¹���ֻ�ܶ�������G��װ�õļӹ�����ÿ��ÿ��ֻ�ܼӹ�4��G��װ�ã�1����ԭ��ÿ�찲��x����������G��װ�ã���������m���¹��ˣ���x��ֵ���ú�m�Ĵ���ʽ��ʾ��2������������Ҫ����������¹��˲����ڹ涨�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ǵ�ĸ�ӣ��������Ϊ�˴����ؽ��羰�������ο��ã���һ�γ�Ϊ180���ؽ��ӵ�����������A��B�����̶��Ⱥ������ɣ�A������ÿ������12�ף�B���̶�ÿ������8�ף�����ʱ20�죮��A��B�����̶ӷֱ����κӵ������ף�
�Ÿ������⣬�ߢŰ��ͬѧ�г��в������ķ��������¡����ݼ�ͬѧ���еķ����飬����ֱ�ָ��δ֪��x��y��ʾ�����壬Ȼ���ڷ����в�ȫ��ͬѧ���еķ����飻
![]() ��x��ʾ________________________��y��ʾ_________________________��
��x��ʾ________________________��y��ʾ_________________________��
�������ͬѧֱ����A���̶����κӵ�������Ϊx��B���̶����κӵ�������Ϊy���г���һ�������飬��A��B�����̶ӷֱ����κӵ������ף����������д�������Ľ����̡�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
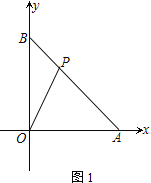
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�A��B����Ϊ(6��0)��(0��6)��PΪ�߶�AB�ϵ�һ��
(1) ��ͼ1����S��AOP��12����P������
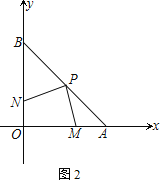
(2) ��ͼ2����PΪAB���е㣬��M��N�ֱ���OA��OB���ϵĶ��㣬��M�Ӷ���A����N�Ӷ���Oͬʱ�����������ǵ��ٶȶ�Ϊ1 cm/s������M��N�˶��Ĺ����У��߶�PM��PN֮���кι�ϵ����֤��
(3) ��ͼ3����PΪ�߶�AB������A��B������һ�㣬��B����BD��OP����OP��OA�ֱ���F��D���㣬EΪOA��һ�㣬�ҡ�PEA����BDO�����ж��߶�OD��AE��������ϵ����˵������
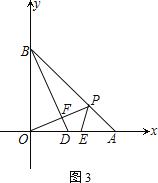
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O�����ߣ�BΪ�е㣬Բ����AC�ϣ���A=30�㣬DΪ ![]() ���е㣮
���е㣮 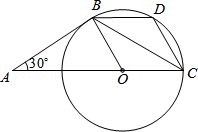
��1����֤��AB=BC��
��2����֤���ı���BOCD�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����OABC����������A��0��10����B��8��10����C��8��0������O��C�����������y=ax2+bx+c���߶�AB���ڵ�D����ֱ��CD�۵�����OABC��һ��BC��ʹ��B����OA���ϵĵ�E����
��1����AD�ij��������ߵĽ���ʽ��
��2��һ����P�ӵ�E��������EC��ÿ��2����λ�����ٶ����C�˶���ͬʱ����Q�ӵ�C��������CO��ÿ��1����λ�����ٶ����O�˶�������P�˶�����Cʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룮���ʵ�tΪ��ֵʱ����P��Q��CΪ������������ǵ��������Σ�
��3������N�������߶Գ����ϣ���M���������ϣ��Ƿ���������ĵ�M���N��ʹ��M��N��C��EΪ�����ı�����ƽ���ı��Σ������ڣ���ֱ��д����M���N�����꣨��д�����̣����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڡ�ABC�У�AB��17��AC��10��BC���ϵĸ�AD��8�����BC�ij�Ϊ( )
A. 21 B. 15 C. 9 D. 9��21
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com