
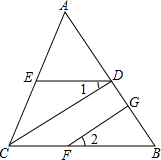
 如图,已知DE∥BC,FG⊥AB,垂足为G,∠1=∠2.
如图,已知DE∥BC,FG⊥AB,垂足为G,∠1=∠2.科目:初中数学 来源: 题型:
 如图,某家设计公司设计了这样一种纸扇:纸扇张开的最大角度θ与360°-θ的比为黄金比,那么制作一把这样的纸扇至少需要用多少平方厘米的纸?(纸扇有两面,结果精确到0.1cm2)
如图,某家设计公司设计了这样一种纸扇:纸扇张开的最大角度θ与360°-θ的比为黄金比,那么制作一把这样的纸扇至少需要用多少平方厘米的纸?(纸扇有两面,结果精确到0.1cm2)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 2x |
| x-1 |
| x |
| x+1 |
| 1 |
| x2-1 |
| 1 |
| x2-2x |
| 1 |
| x2-4x+4 |
| 2 |
| x2-2x |
| m-2-m-1 |
| m-2-2m-1+1 |
| m-2-m-1-2 |
| m-2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 把自然数1到200按如图所示方式排列,用如图所示的长方形框可以围住2×3个数.
把自然数1到200按如图所示方式排列,用如图所示的长方形框可以围住2×3个数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com