
已知二次函数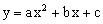 图象的顶
图象的顶 点横坐标是4,与x轴交于A(x1,0)、B(x2,0),x1﹤0﹤x2,与y轴交于点C,O为坐标原点,
点横坐标是4,与x轴交于A(x1,0)、B(x2,0),x1﹤0﹤x2,与y轴交于点C,O为坐标原点,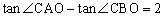 。
。
(1)求证:  ;
;
(2)求a、b的值;
(3)若二次函数图象与直线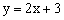
 仅有一个交点时,求二次函数的最值。
仅有一个交点时,求二次函数的最值。
(1)∵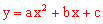 图象的顶点横坐标是4,
图象的顶点横坐标是4,
∴抛物线的对称轴为x=4, 即
即 ,化简得:
,化简得: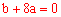 。
。
(2)∵二次函数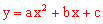 与x轴交于A(x1,0)、B(x2,0),x1<0<x2,
与x轴交于A(x1,0)、B(x2,0),x1<0<x2,
∴OA=-x1,OB=x2;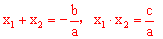 。
。
令x=0,得y =c,∴C(0,c),∴OC=|c|。
=c,∴C(0,c),∴OC=|c|。
由三角函数定义得:
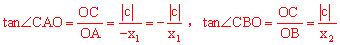 。
。
∵tan∠CAO-tan∠CBO=2,即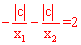 ,化简得:
,化简得: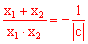 。
。
将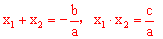 代入得:
代入得: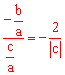 ,化简
,化简 得:
得: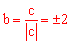 。
。
由(1)知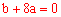 ,
,
∴当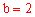 时,
时,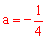 ;当
;当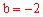 时,
时,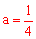 。
。
∴a、b的值为: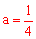 ,
, 或
或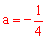 ,
,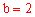 。
。
(3)①由(2)知,当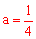 ,
, 时,抛物线解析式为:
时,抛物线解析式为: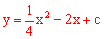 。
。
联立抛物线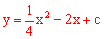 与直线
与直线 解析式得到:
解析式得到: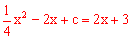 ,
,
化简得: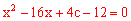 。
。
∵二次函数图象与直线 仅有一个交点,
仅有一个交点,
∴一元二次方程根的判别式 等于0,即
等于0,即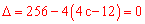 ,解得
,解得 =19。
=19。
∴抛物线解析式为: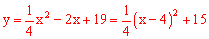 。
。
当x=4时,二次函数有最小值,最小值为15。
②由(2)知,当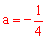 ,
,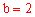 时,抛物线解析式为:
时,抛物线解析式为: 。
。
联立抛物线 与直线
与直线 解析式得到:
解析式得到: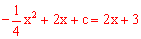 ,
,
化简得 :
: 。
。
∵二次函数图象与直线 仅有一个交点,
仅有一个交点,
∴一元二次方程根的判别式等于0,即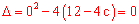 ,解得
,解得 =3。
=3。
∴抛物线解析式为: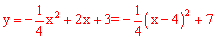 。
。
当x=4时,二次函数有最大值,最大值为7。
综上所述,若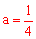 ,
, ,
, =19,二次函数图象与直线
=19,二次函数图象与直线 仅有一个交点时,二次函数的最小值为15;若
仅有一个交点时,二次函数的最小值为15;若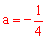 ,
,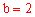 ,
, =3,二次函数图象与
=3,二次函数图象与 直线
直线 仅有一个交点时,二次函数的最大值为7。
仅有一个交点时,二次函数的最大值为7。
【考点】二次函数综合题,曲线上点的坐标与方程的关系,一元二次方程根的判别式和根与系数的关系,锐角三角函数定义,二次函数的性质,分类思想的应用。



 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
如图,反比例函数
 的图象与正比例函数
的图象与正比例函数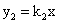
 的图象交于点(2,1),则使y1>y2的x的取值范围是【 】
的图象交于点(2,1),则使y1>y2的x的取值范围是【 】


A.0<x<2 B.x>2 C.x>2或-2<x<0 D.x<-2或0<x<2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,平行四边形ABCD中,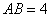
 ,点
,点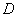
 的坐标是
的坐标是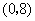
 ,以点
,以点
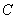
 为顶点的抛物线
为顶点的抛物线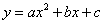
 经过
经过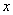
 轴上的点
轴上的点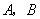
 .
.


(1)求点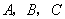
 的坐标;
的坐标;
(2)若抛物线向上平移后恰好经过点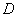
 ,求平移后抛物线的解析式.
,求平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
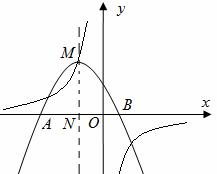
如图,已知二次函数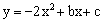 图像的顶点M在反比例函数
图像的顶点M在反比例函数 上,且与
上,且与 轴交于A,B两点。
轴交于A,B两点。
(1)若二次函数的对称轴为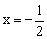 ,试
,试 求
求 的值,并求AB的长;
的值,并求AB的长;
(2)若二次函数的对称轴在 轴左侧,与
轴左侧,与
 轴的交点为N,当NO+MN取最小值时,试求二次函数的解析式。
轴的交点为N,当NO+MN取最小值时,试求二次函数的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整,原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若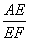
 =3,求
=3,求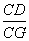
 的值.
的值.
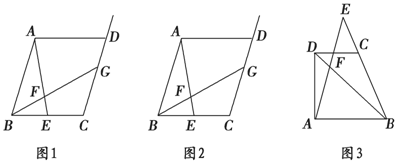

(1)尝试探究 :
:
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是________,
CG和EH的数量关系是________,
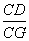
 的值是________.
的值是________.
(2)类比延伸:
如图2,在原题条件下,若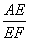
 =m(m>0)则
=m(m>0)则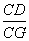

 的值是________(用含有m的代数式表示),试写出解答过程.
的值是________(用含有m的代数式表示),试写出解答过程.
(3)拓展迁移:
如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F,若
 =a,
=a,
 =b(a>0,b>0)则
=b(a>0,b>0)则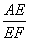
 的值是________(用含a、b的代数式表示).
的值是________(用含a、b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠C=90°,∠A=45°,AB=2.将△ABC绕顶点A顺时针方向旋转至△ AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .
AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com