
如图,平行四边形ABCD中,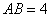
 ,点
,点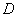
 的坐标是
的坐标是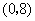
 ,以点
,以点
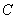
 为顶点的抛物线
为顶点的抛物线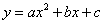
 经过
经过
 轴上的点
轴上的点
 .
.


(1)求点
 的坐标;
的坐标;
(2)若抛物线向上平移后恰好经过点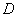
 ,求平移后抛物线的解析式.
,求平移后抛物线的解析式.
科目:初中数学 来源: 题型:
图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②.其中AN表示平板电脑,M为AN上的定点,AN=CB=20 cm,AM=8 cm,MB=MN.我们把∠ANB叫做倾斜角.
(1)当倾斜角为45°时,求CN的长;
(2)按设计要求,倾斜角能小于30°吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图 象描述如图所示,有下列结论:①火车的速度为30米/秒; ②火车的长度为120米;③火
象描述如图所示,有下列结论:①火车的速度为30米/秒; ②火车的长度为120米;③火 车整体都在隧道内的时间为35秒;
车整体都在隧道内的时间为35秒; ④隧道长度为1200米。
④隧道长度为1200米。
其中正确的结论是 .(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx+c,小王骑自行车从O匀速沿直线到拱梁一端A,再匀速通过拱梁部分的桥面AC,小王从O到A用了2秒, 当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面AC共需
当小王骑自行车行驶10秒时和20秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面AC共需  秒.
秒.


查看答案和解析>>
科目:初中数学 来源: 题型:
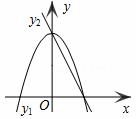
如图,已知抛物线y1=﹣2x2+2,直线y2=﹣2x+2,当x任取一值时,x对应的函数值分别为y1、y 2.若y1≠y2,取y1、y2中的较大值记为M;若y1=y2
2.若y1≠y2,取y1、y2中的较大值记为M;若y1=y2 ,记M=y1=y2。例如:当x=﹣1时,y1=0,y2=4,y1<y2,此时M=4。下列判断:
,记M=y1=y2。例如:当x=﹣1时,y1=0,y2=4,y1<y2,此时M=4。下列判断:
①当 x<0时,y1>y2;
x<0时,y1>y2;
②当x>0时,x值越大,M值越小;
③当x≥0时,使得M大于2的x值不存在;
④使得M=1的x值是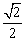 。
。
其中正确的有【 】
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数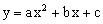 图象的顶
图象的顶 点横坐标是4,与x轴交于A(x1,0)、B(x2,0),x1﹤0﹤x2,与y轴交于点C,O为坐标原点,
点横坐标是4,与x轴交于A(x1,0)、B(x2,0),x1﹤0﹤x2,与y轴交于点C,O为坐标原点,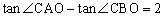 。
。
(1)求证:  ;
;
(2)求a、b的值;
(3)若二次函数图象与直线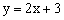
 仅有一个交点时,求二次函数的最值。
仅有一个交点时,求二次函数的最值。
查看答案和解析>>
科目:初中数学 来源: 题型:
定义:如果一个y与x的函 数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如:
数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如: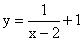
 的图象向左平移2个单位,再向下平移1个单位得到
的图象向左平移2个单位,再向下平移1个单位得到
 的图象,则
的图象,则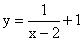
 是y与x的“反比例平移函数”.
是y与x的“反比例平移函数”.
(1)若矩形的两边分别是2cm、3cm,当这两边分别增加x(cm)、y(cm)后,得到的新矩形的面积为8cm2,求y与x的函数表达式,并判断这个函数是否为“反比例平移函数”.
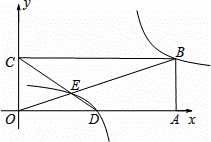
(2)如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3).点D是OA的中点,连接OB、CD交于点E,“反比例平移函数”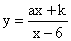
 的图象经过B、E两点.则这
的图象经过B、E两点.则这 个“反比例平移
个“反比例平移 函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.
函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.
(3)在(2)的条件下,已知过线段BE中点的一条直线l交这个“反比例平移函数”图象于P、Q两点(P在Q的右侧),若B、E、P、Q为顶点组成的四边形面积为16,请求出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com