
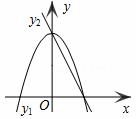
如图,已知抛物线y1=﹣2x2+2,直线y2=﹣2x+2,当x任取一值时,x对应的函数值分别为y1、y 2.若y1≠y2,取y1、y2中的较大值记为M;若y1=y2
2.若y1≠y2,取y1、y2中的较大值记为M;若y1=y2 ,记M=y1=y2。例如:当x=﹣1时,y1=0,y2=4,y1<y2,此时M=4。下列判断:
,记M=y1=y2。例如:当x=﹣1时,y1=0,y2=4,y1<y2,此时M=4。下列判断:
①当 x<0时,y1>y2;
x<0时,y1>y2;
②当x>0时,x值越大,M值越小;
③当x≥0时,使得M大于2的x值不存在;
④使得M=1的x值是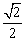 。
。
其中正确的有【 】
A.1个 B.2个 C.3个 D.4个
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
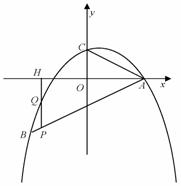
如图,二次函数y=-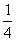 x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
(1)求此二次函数的解析式;
(2)证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图像及x轴于Q、H两点,试问:是否存在这样的点 P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
在青岛市开展的创城活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园
 ,花园的一边靠墙,另三边用总长为40m的栅栏围
,花园的一边靠墙,另三边用总长为40m的栅栏围 成(如图所示).若设花园的
成(如图所示).若设花园的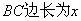
 (m),花园的面积为
(m),花园的面积为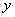

 (m
(m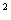
 ).
).
(1)求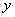
 与
与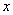
 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量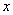
 的取值范围;
的取值范围;
(2)满足条件的花园面积能达到200 m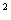
 吗?若能,求出此时
吗?若能,求出此时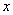
 的值;若不能,说明理由;
的值;若不能,说明理由;
(3)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当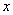
 取何值时,花园的面积最大?最大面积为多少?
取何值时,花园的面积最大?最大面积为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,平行四边形ABCD中,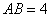
 ,点
,点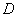
 的坐标是
的坐标是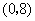
 ,以点
,以点
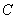
 为顶点的抛物线
为顶点的抛物线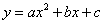
 经过
经过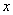
 轴上的点
轴上的点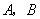
 .
.


(1)求点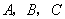
 的坐标;
的坐标;
(2)若抛物线向上平移后恰好经过点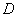
 ,求平移后抛物线的解析式.
,求平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
若关于x的一元二次 方程
方程 有实数根x1,x2,且x1≠x2,有下列结论:
有实数根x1,x2,且x1≠x2,有下列结论:
①x1=1,x2=2; ②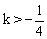 ;
;
③二次函数y= 的图象与x轴交点的坐标
的图象与x轴交点的坐标 为
为 (1,0)和(2,0)。
(1,0)和(2,0)。
其中,正确结论的个数是【 】
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,矩形ABCD中,AB=6,BC=8,点E、F分别是BC、CD边上的点,且AE⊥EF,BE=2,
(1)求证:AE=EF;
(2)延长EF交矩形∠BCD的外角平分线C
 P于点P(图2),试求AE与EP的数量关系;
P于点P(图2),试求AE与EP的数量关系;

查看答案和解析>>
科目:初中数学 来源: 题型:
已知,大正方形的边长为4 ,小正方形的边长为2
,小正方形的边长为2 ,状态如图所示.大正方形固定不动,把小正方形以
,状态如图所示.大正方形固定不动,把小正方形以 的速度向大正方形的内部沿直线平移,设平移的时间为
的速度向大正方形的内部沿直线平移,设平移的时间为 秒,两个正方形重叠部分的面积为
秒,两个正方形重叠部分的面积为
 ,完成下列问题:
,完成下列问题:
(1).用 含
含 的式子表示
的式子表示 ,要求画出相应的图形,表明
,要求画出相应的图形,表明 的范围;
的范围;
(2).当 ,求重叠部分的面积
,求重叠部分的面积 ;
;
(3).当
 ,求
,求 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com