如图1，矩形ABCD中，AB=6，BC=8，点E、F分别是BC、CD边上的点，且AE⊥EF，BE=2，
（1）求证：AE=EF；
（2）延长EF交矩形∠BCD的外角平分线C
P于点P（图2），试求AE与EP的数量关系；
（1）∵AE⊥EF，∴∠BEA+∠CEF=90°。
∵四边形ABCD为矩
形，∴∠B=∠C=90°。
∴∠BAE +∠BEA =90°。∴∠BA E=∠CEF。
又∵AB=DC=6，BC=8，BE=2，∴AB=EC=6。
∴△ABE≌△ECF（ASA）。
∴AE=EF。
（2）如图，在AB上取一点M，使BM=BE，
连接ME。
∴AM=CE。
∴∠BME=45°。∴∠AME=135°。
∵CP是外角平分线，∴∠
DCP=45°。∴∠ECP=135°。
∴∠AME=∠ECP。
由（1）知∠MA E=∠CEP
，
∴△AME∽△ECP。∴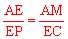
。
∵AM=2，EC=3，∴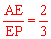
。
∴AE与EP的数量关系是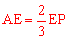
。
【考点】矩形的性质，全等三角形的判定和性质，外角平分线定义，相似三角形的判定和性质。
能力评价系列答案
唐印文化课时测评系列答案科目：初中数学 来源： 题型：
如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=
8cm．点D、E、F分别是
边AB，BC，AC的中点，连接DE，DF，动点P，Q分别从点A、B同时出发，运动速度均为1cm/s，点P沿AFD的方向运动到点D停止；
点Q沿BC的方向运动，当点P停止运动时，点Q
也停止运动．在运动过程中，过点Q作BC的垂线交AB于点M，以点P，M，Q为顶点作平行四边形PMQN．设平行四边形边形PMQN与矩形FDEC重叠部分的面积为y（cm2）（这里规定线段是面积为0有几何图形），点P运动的时间为x（s）
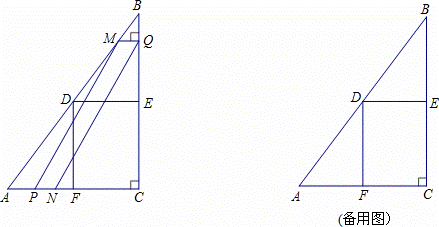
（1）当点P运动到点F时，CQ= cm；
（2）在点P从点F运动到点D的过程中，某一时刻，点P落在MQ上，求此时BQ的长度；
（3）当点P在线段FD上运动时，求y与x之间的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
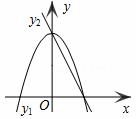
如图，已知抛物线y1=﹣2x2+2，直线y2=﹣2x+2，当x任取一值时，x对应的函数值分别为y1、y
2．若y1≠y2，取y1、y2中的较大值记为M；若y1=y2
，记M=y1=y2。例如：当x=﹣1时，y1=0，y2=4，y1＜y2，此时M=4。下列判断：
①当
x＜0时，y1＞y2；
②当x＞0时，x值越大，M值越小；
③当x≥0时，使得M大于2的x值不存在；
④使得M=1的x值是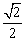
。
其中正确的有【 】
A．1个 B．2个 C．3个 D．4个
查看答案和解析>>
科目：初中数学 来源： 题型：
已知A，B，C为⊙O上相邻的三个六等分点，点E在劣弧AC上(不与A，B，C重合)，EF
为⊙O的直径，将⊙O沿EF折叠，使点A与A′重合，点B与B′重合，连接EB′，EC，EA′。设EB′=b，EC=c，EA′=p。试探究b，c，p三者的数量关系。
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，平面之间坐标系中，Rt△ABC的∠ACB=90º，∠CAB=30º，直角边BC在x轴正半轴上滑动，点C的坐标为（t，0），直角边AC=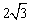
，经过O，C两点做抛物线
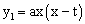（a为常数，a＞0），该抛物线与斜边AB交于点E，直线OA：y2=kx（k为常数，k＞0）
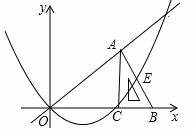
（1）填空：用含t的代数式表示点A的坐标及k的值：A ，k= ；
（2）随着三角板的滑动，当a=1时：
①请你验证：抛物
线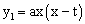
的顶点在函数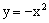
的图象上；
②当三角板滑至点E为AB的中点时，求t
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
知⊙B与△ABD的边A
D相切于点C，AC=
，⊙B的半径为2，当⊙A与⊙B相切时，⊙A
的半径是【 】
1 
3 
2
1或3