
如图,二次函数y=-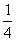 x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
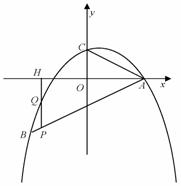
(1)求此二次函数的解析式;
(2)证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图像及x轴于Q、H两点,试问:是否存在这样的点 P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)y=-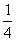 x2+
x2+ x+2;(2)证明见解析;(3)(-1,-
x+2;(2)证明见解析;(3)(-1,-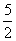 )与(-3,-
)与(-3,-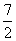 ).
).
【解析】(1)∵点A(4,0)与B(-4,-4)在二次函数图像上,
∴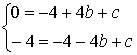 ,解得
,解得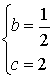 ,∴二次函数解析式为y=-
,∴二次函数解析式为y=-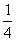 x2+
x2+ x+2.
x+2.
(2)过B作BD⊥x轴于点D,由(1)得C(0,2)
在Rt△AOC中,tan∠CAO=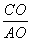 =
=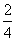 =
= ,
,
在Rt△ABD中,tan∠BAD=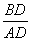 =
=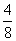 =
= ,
,
∵tan∠CAO= tan∠BAD ,∴∠CAO=∠BAD
(3)由A(4,0)与B(-4,-4),可得直线AB的解析式为y= x-2,
x-2,
设P(x, x-2),(
x-2),(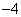 <
<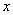 <4),则Q(x,-
<4),则Q(x,-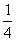 x2+
x2+ x+2),
x+2),
∴PH=| x-2|=2-
x-2|=2- x QH=|-
x QH=|-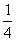 x2+
x2+ x+2|.
x+2|.
∴2- x =2|-
x =2|-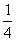 x2+
x2+ x+2|
x+2|
当2- x =-
x =- x2+x+4, 解得 x1=-1,x2=4(舍去),∴P(-1,-
x2+x+4, 解得 x1=-1,x2=4(舍去),∴P(-1,-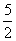 )
)
当2- x =
x = x2-x-4, 解得x1=-3,x2=4(舍去),∴P(-3,-
x2-x-4, 解得x1=-3,x2=4(舍去),∴P(-3,-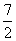 )
)
综上所述,存在满足条件的点,它们是(-1,-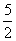 )与(-3,-
)与(-3,-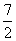 ).
).


科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,坐标原点为O,A点坐标为(4,0),B点坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P的正半轴交于点C.

(1)求经过A、B、C三点的抛物线所对应的函数解析式;
(2)设M为(1)中抛物线的顶点,求直线MC对应的函数解析式;
(3)试说明直线MC与⊙P的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②.其中AN表示平板电脑,M为AN上的定点,AN=CB=20 cm,AM=8 cm,MB=MN.我们把∠ANB叫做倾斜角.
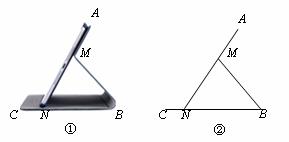
(1)当倾斜角为45°时,求CN的长;
(2)按设计要求,倾斜角能小于30°吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
某农户种植花生,原来种植的花生亩产量为200千克,出油率为50%(即每100千克花生可加工成花生油50千克).现在种植新品种花生后,每亩收获的花生可加工成花生油132千克,其中花生出油率的增长率是亩产量的增长率的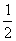 .则新品种花生亩产量的增长率为
.则新品种花生亩产量的增长率为
A、20% B、30% C、50% D、120%
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC= 8cm.点D、E、F分别是
8cm.点D、E、F分别是 边AB,BC,AC的中点,连接DE,DF,动点P,Q分别从点A、B同时出发,运动速度均为1cm/s,点P沿AFD的方向运动到点D停止;
边AB,BC,AC的中点,连接DE,DF,动点P,Q分别从点A、B同时出发,运动速度均为1cm/s,点P沿AFD的方向运动到点D停止; 点Q沿BC的方向运动,当点P停止运动时
点Q沿BC的方向运动,当点P停止运动时 ,点Q
,点Q 也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形边形PMQ
也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形边形PMQ N与矩形FDEC重叠部分的面积为y(cm2)(这里规定线段是面积为0有几何图形),点P运动的时间为x(s)
N与矩形FDEC重叠部分的面积为y(cm2)(这里规定线段是面积为0有几何图形),点P运动的时间为x(s)
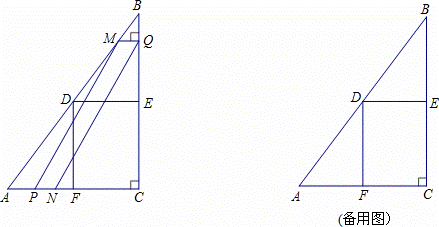
(1)当点P运动到点F时,CQ= cm;
(2)在点P从点F运动到点D的过程中,某一时刻,点P落在MQ上,求此时BQ的长度;
(3)当点P在线段FD上运动时,求y与x之间的函数关 系式.
系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
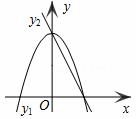
如图,已知抛物线y1=﹣2x2+2,直线y2=﹣2x+2,当x任取一值时,x对应的函数值分别为y1、y 2.若y1≠y2,取y1、y2中的较大值记为M;若y1=y2
2.若y1≠y2,取y1、y2中的较大值记为M;若y1=y2 ,记M=y1=y2。例如:当x=﹣1时,y1=0,y2=4,y1<y2,此时M=4。下列判断:
,记M=y1=y2。例如:当x=﹣1时,y1=0,y2=4,y1<y2,此时M=4。下列判断:
①当 x<0时,y1>y2;
x<0时,y1>y2;
②当x>0时,x值越大,M值越小;
③当x≥0时,使得M大于2的x值不存在;
④使得M=1的x值是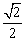 。
。
其中正确的有【 】
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com