
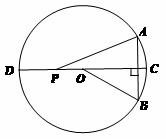
如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,连接PA,则∠PAB的度数可以是 (写出一个即可)
科目:初中数学 来源: 题型:
如图,在⊿ABC中,∠A﹤90°,∠C=30°,AB=4,BC=6,E为AB的中点,P为AC边上一动点,将⊿ABC绕点B逆时针旋转 角(
角( )得到
)得到 ,点P的对应点为
,点P的对应点为
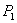 ,连
,连 ,在旋转过程中,线段
,在旋转过程中,线段 的长度的最小值是 .
的长度的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
正方形ABCD中,点P从点C出发沿着正方形的边依次经过点D,A向终点B运动,运动的路程为x(cm),△PBC的面积为y(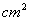 ),y随x变化的图象可能是( )
),y随x变化的图象可能是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
在矩形ABCD中,AB=1,AD=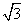 ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE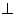 BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
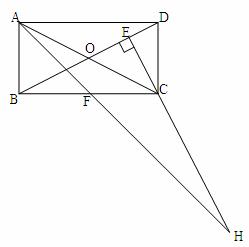
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形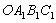 的边长为2,以
的边长为2,以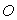 为圆心、
为圆心、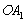 为半径作弧
为半径作弧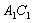 交
交 于点
于点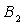 ,设弧
,设弧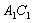 与边
与边 、
、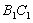 围成的阴影部分面积为
围成的阴影部分面积为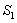 ;然后以
;然后以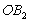 为对角线作正方形
为对角线作正方形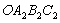 ,又以
,又以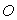 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交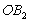 于点
于点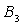 ,设弧
,设弧 与边
与边 、
、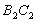 围成的阴影部分面积为
围成的阴影部分面积为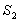 ;…,按此规律继续作下去,设弧
;…,按此规律继续作下去,设弧 与边
与边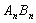 、
、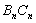 围成的阴影部分面积为
围成的阴影部分面积为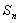 .则:(1)
.则:(1)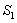 = ;(2)
= ;(2)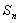 = .
= .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,二次函数y=-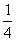 x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
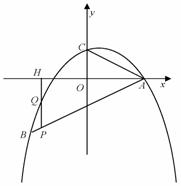
(1)求此二次函数的解析式;
(2)证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图像及x轴于Q、H两点,试问:是否存在这样的点 P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
在青岛市开展的创城活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园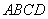
 ,花园的一边靠墙,另三边用总长为40m的栅栏围
,花园的一边靠墙,另三边用总长为40m的栅栏围 成(如图所示).若设花园的
成(如图所示).若设花园的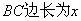
 (m),花园的面积为
(m),花园的面积为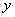

 (m
(m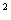
 ).
).
(1)求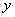
 与
与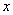
 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量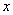
 的取值范围;
的取值范围;
(2)满足条件的花园面积能达到200 m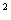
 吗?若能,求出此时
吗?若能,求出此时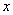
 的值;若不能,说明理由;
的值;若不能,说明理由;
(3)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当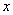
 取何值时,花园的面积最大?最大面积为多少?
取何值时,花园的面积最大?最大面积为多少?
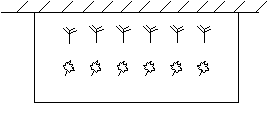

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com